The main characteristic of the GEKO model is that it has several free parameters for tuning the model to different flow scenarios. The starting point for the formulation is:

(12–114)

(12–115)

(12–116)

(12–117)

(12–118)

(12–119)

(12–120)

with

The free coefficients of the GEKO model are implemented through the functions (,, ) which can be tuned by the user to achieve different goals in different parts of the simulation domain. Currently there are six parameters included for that purpose:

All coefficients (except of which is of minor importance) can be accessed globally or locally through User Defined Functions (UDFs), allowing a global or zonal model optimization.

The coefficients and affect boundary layers, whereas and are designed for free shear flows. In order to avoid any influence of and onto boundary layers, a blending function is introduced, which de-activates and in the boundary layer. The function is similar to the blending function used in the BSL/SST model formulation and given by:

(12–121)

This function activates the free shear flow parameters as follows:

(12–122)

There are two important aspects. Firstly, the function =1 inside boundary layers and =0 for free shear flows. Secondly, the parameter is a sub-parameter of . It only affects the simulation in case 0.

The free coefficients should be in the range (defaults in parenthesis):

The greyed values for are only suggestions. There might be situations where values higher than 1.0 can be appropriate.

As mentioned above, for the coefficient a correlation is provided as default, which ensures that changes in do not negatively affect free mixing layers:

(12–123)

It is well-known that any conventional two-equation model exhibits build-up of turbulence in stagnation regions of bluff bodies (like leading edges of airfoils etc.). The reason lies in the substitution of the eddy-viscosity assumption into the production term of the two-equation model. The eddy-viscosity assumption is not representing the physics correctly in such regions and leads to an over-production of turbulence kinetic energy, which in turn can lead to excessive eddy-viscosity levels in these areas. This can have a detrimental effect on the flow over the rest of the geometry, as the boundary layers starting from the leading edge stagnation point would be predicted incorrectly. This can cause large errors and even false separation. Such situations do not only appear in classical stagnation zones of airfoils, but in many technical flows, where flows hit on a surface or different flow streams collide to form a stagnation region.

There are numerous remedies for that problem. The most widely known is the use of the so-called Kato-Launder correction [15] whereby the square of the shear strain in is replaced by strain times vorticity:

(12–124)

This option is available, albeit typically not by default. It is however activated when using the GEKO model in combination with a model for laminar-turbulent transition, as it prevents even small production rates which can have a significant effect on transitional flows. It should be noted that the Kato-Launder modification can have an effect on flows with rotation and swirl relative to the original model calibration. It also leads to un-physical production in rotating systems as pointed out by Durbin and Reif [11] and should therefore be applied with caution.

An alternative was proposed by Menter [17] in form of a production limiter:

(12–125)

The limiting coefficient can be chosen fairly large (typically =10), relative to the equilibrium relation . It will therefore not affect any calibrated flow and still avoids the stagnation build-up and is used as a default option in GEKO (as in all other based models in Ansys CFD).

A more theoretical concept can also be applied by imposing a realizability constraint. Realizability demands e.g. that all normal Reynolds Stress components need to always remain positive (e.g. [11]). This is clearly true from a physical standpoint, but can be violated by eddy-viscosity models (as well as EARSM and RSM). One can argue about how important this constraint is from a practical standpoint, as eddy-viscosity models do not attempt to accurately describe each single Reynolds Stress, but model essentially the principal shear stress. Still, the realizability constraint can, as a side-effect, help to avoid stagnation build up. For eddy-viscosity models it reads:

(12–126)

The realizability limiter has the additional benefit to prevent numerical break-down in case approaches zero at any point in the domain. Without the constraint in the denominator, this would lead to arbitrarily high eddy-viscosities, whereas with the limiter, such points are typically handled gracefully.

In the GEKO model the realizability limiter is utilized in addition to the production limiter by default. Users can change the values of both coefficients.

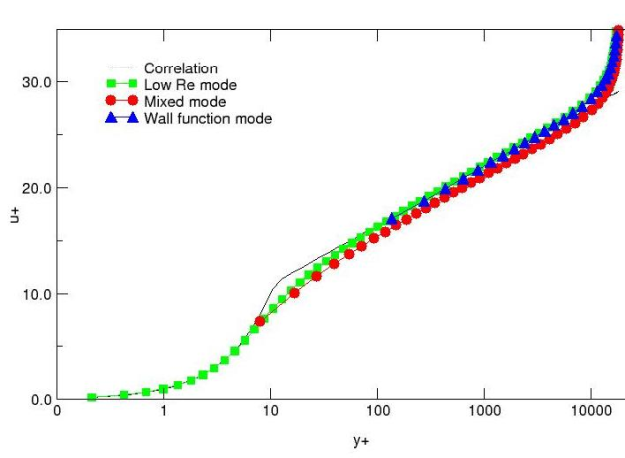
The near wall formulation of a turbulence model has a substantial effect on its accuracy and its robustness. In addition, modern CFD codes typically feature so-called -insensitive wall formulations, which allow the user to obtain sensible simulations over a wide range of grids with different near wall resolutions.

The GEKO model family was designed by sticking closely to the original model formulation – following the argument that the modeled is proportional to and not to the physical turbulence kinetic energy. The peak observed in the turbulence kinetic energy in the buffer layer is therefore not modelled, as it consists mostly of passive motion (no effect on shear stress).

A -insensitive wall formulation has been developed for the GEKO model (similar to what is used in the BSL and SST models). It allows the use of the model, on meshes of arbitrary values, as long as the -value lies in the logarithmic layer of the boundary layer, and as long as the rest of the boundary layer is resolved with a sufficient number of cells.

Figure 12.170: Near wall insensitive wall treatment for GEKO model.

The -insensitive wall formulation has the advantage that users do not have to select a wall treatment. The optimal formulation is selected by the formulation based on the grid provided.

It is important to counter a widely held belief that based models require a finer near wall resolution than say a model with wall functions. This is not correct, as the -insensitive wall formulation blends to the exact same wall function once the grid is coarsened.

In order to demonstrate the superior behavior of based models compared with other models, a backstep was computed on a y+~1 mesh. The wall shear stress and Stanton number (heat transfer) distribution downstream of the step are shown in Figure 12.171: Wall shear stress coefficient, (left) and wall heat transfer coefficient, St, (right) for backward-facing step flow [31]. All curves are based on the same high Re number model (the GEKO model is set to an exact transformation of ). The ML is a low Re number model, EWT is a 2-layer formulation [35] and the V2f model is an extension of with elliptic blending [12]. While all baseline models are essentially identical, the differences in near wall formulation results in very large differences between the results. It is obvious that the GEKO model is closest to the experimental data.

Figure 12.171: Wall shear stress coefficient, (left) and wall heat transfer coefficient, St, (right) for backward-facing step flow [31]

In order to clearly characterize the model variant used in an application, it is important to have a unified terminology for the model. It is proposed to just name the coefficients which are not default.