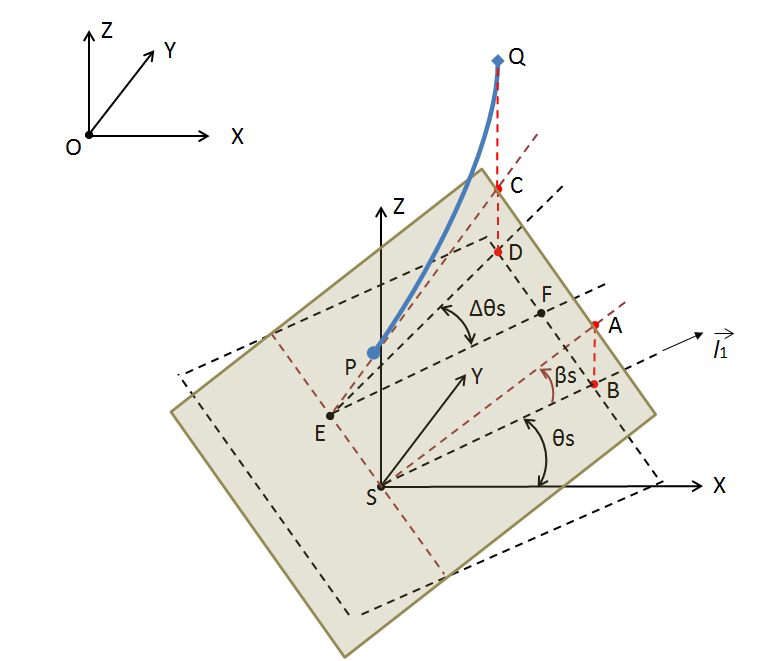
A global sloped seabed can be defined for quasi-static composite cable analysis.
As shown in Figure 9.7: Global Sloped Seabed Definition, a local seabed right-hand
Cartesian frame SXYZ is defined, in which the origin is on the seabed reference point and the local axes are parallel to the corresponding axes of the fixed
reference axes. The seabed slope angle
is the angle between the steepest upward path on the seabed and the horizontal
plane. The seabed azimuth angle
is the angle between the projection of the steepest path on the horizontal
plane and the local x-axis.
To express the relevant geometric information of the seabed and the composite cable, point
A is designated as a point on the line passing through a reference point S and being in the
steepest upward direction on the seabed. Point B is the intersection point between the
horizontal SXY plane and the vertical line across point A. The angle between line SA and line SB
defines the seabed slope angle , the angle between line SB and the x-axis of SXYZ gives the seabed azimuth
angle
.
By denoting the anchor point on the seabed as P: in the global fixed reference frame, the following equation is
satisfied:
(9–39) |
where is the seabed azimuth directional vector in the fixed reference axes.
Assuming that the attachment point of a composite mooring Q: is above the seabed but not on the vertical line across point P, the mooring
vertical plane which point P and point Q are on can be uniquely determined. Defining the
vertical line across point Q, this line has an intersection point with the seabed at point C and
an intersection point with the SXY plane at point D. Point E is the intersection point of the
SXY plane and the line crossing points C and P. Line EF parallels to line SB, and the relative
azimuth angle of the mooring vertical plane and the seabed direction is
.
Based on the definitions above, the coordinate of point C: is determined by:
(9–40) |
The coordinate of point D: is:
(9–41) |
and the coordinate of point E: is:
(9–42) |
In the general case of , the relative azimuth angle of the mooring vertical plane is given by:
(9–43) |
where
|
|
|
|
From Equation 9–42 it can be observed that point E does not
exist if . In this special case, the relative azimuth angle of the mooring vertical
plane is:
(9–44) |