Benchmark D2

VMD2
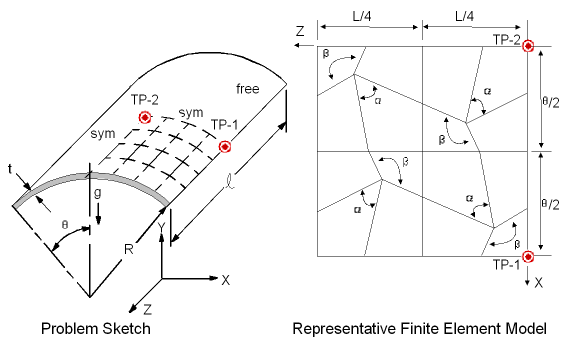
Barrel Vault Roof Under Self Weight

Overview

Reference:

R. D. Cook, Concepts and Applications of Finite Element Analysis, 2nd Edition, John Wiley and Sons, Inc., 1981, pp. 284-287.

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Element Type(s):

4-Node Finite Strain Shell Elements (SHELL181)

8-Node Finite Strain Shell Elements (SHELL281)

Input Listing:

vmd2.dat

Test Case

A cylindrical shell roof is subjected to gravity loading. The roof is supported by walls at each end and is free along the sides. Monitor the y-displacement and bottom axial stress (σ_z) at target point 1 along with the bottom circumference stress (σ_θ) at target point 2 for a series of test cases with varying skew angle β for each element type. A companion problem that studies uniform element mesh refinement is VMC3.

Figure 605: Cylindrical Shell Roof Problem Sketch

Material Properties

Geometric Properties

Loading and Boundary Conditions

E = 4.32 x 10⁸ N/m²

υ = 0.0

ρ = 36.7347 kg/m³

Parameter Definitions

β = Skew Angle

L = 50 m

R = 25 m

t = 0.25 m

Θ = 40°

g = 9.8 m/sec²

At x = 0 Symmetric

At z = 0 Symmetric

At x = L UX = UY = ROTZ = 0

Representative Mesh Options

Target Solution

Target solution is obtained using a uniform 8 x 8 quadrilateral mesh of an 8-node quadrilateral shell element, (see R. D. Cook, Concepts and Applications of Finite Element Analysis).

ETYP	Beta (Deg.)	Alpha (Deg.)	UY (1), in	Axial Stress (1) Bottom,kPa	Hoop Stress (2) Bottom,kPa
--	90	90	-.3016	358.42	-213.40

Results Comparison - Quadrilateral Elements

			Ratio
ETYP	Beta	Alpha	UY (1)	Axial Stress (1) Bottom	Hoop Stress (2) Bottom
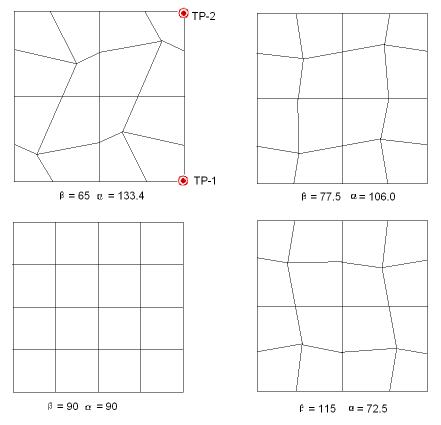
181	65	133.4	1.019	0.946	0.918
181	77.5	106	1.037	0.950	0.965
181	90	90	1.048	0.940	0.983
181	110	75.1	1.056	0.910	0.956
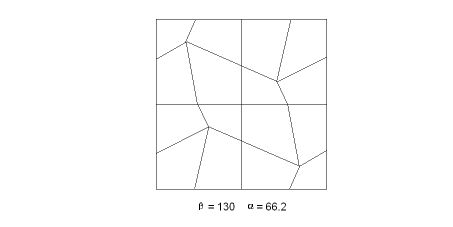
181	130	66.2	1.055	0.863	0.889
281	65	133.4	0.974	0.985	1.133
281	77.5	106	0.999	0.967	1.049
281	90	90	1.004	0.953	1.027
281	110	75.1	0.994	0.949	1.049
281	130	66.2	0.971	0.960	1.059

Assumptions, Modeling Notes, and Solution Comments

The problem is designed to test singly-curved shell elements under combined membrane and bending deformation. The solid model is set up to produce irregular element shapes for quadrilateral elements. The angle β is prescribed, while the angle α is calculated from the resulting geometry. The range of β is set such that all element interior angles fall within 90° ± 45°.
The target solution is obtained from the author's 8-node shell element, (see R. D. Cook, Concepts and Applications of Finite Element Analysis), under a uniform rectangular element geometry using an 8 x 8 mesh pattern.
Results for uniform quadrilateral element shapes are noted in the tabular and graphical output for β = 90° and should be used as a basis for comparison of distorted element performance.
Displacement results over the range of element distortion vary the greatest for SHELL181. In this problem, SHELL281 predict the displacements more accurately for mild element geometry distortion.
Axial (σ_z) stress results, over the range of element distortion, show some variation for SHELL181, and SHELL281 elements. Hoop (σ_θ) stress results are less affected by irregular element shapes except at the extreme β angle range.