Benchmark D3

VMD3
Free-Free Vibration of a Solid Beam

Overview

Reference:

R. D. Blevins, Formulas for Natural Frequency and Mode Shape, Van Nostrand Reinhold Co., New York, NY, 1979, Tables 8-1 and 8-16.

Analysis Type(s):

Mode-frequency analysis (ANTYPE = 2)

Element Type(s):

2D 4-Node Structural Solid Elements (PLANE182)

2D 8-Node Structural Solid Elements (PLANE183)

3D 8-Node Structural Solid Elements (SOLID185)

3D 20-Node Structural Solid Elements (SOLID186)

3D 10-Node Tetrahedral Structural Solid Elements (SOLID187)

Input Listing:

vmd3.dat

Test Case

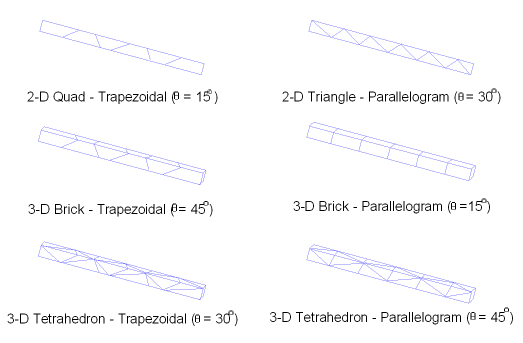
A free-free solid beam is analyzed to determine the first axial and bending mode natural frequencies. The axial and bending modes are extracted using the Block Lanczos eigenvalue extraction method. Examine the influence of rectangular, trapezoidal, and parallelogram element shape models on the eigenvalue calculations.

Figure 606: Free-Free Solid Beam Problem Sketch

Material Properties

Geometric Properties

Loading and Boundary Conditions

E = 200 x 10⁹ N/m²

υ = 0.3

ρ = 8000 kg/m³

L = 12 m

d = 0.1 m

t = 0.2 m

Parameter Definitions

Θ = Element Distortion Angle

At X = L/2 UX = 0

At Z = 0 UZ = 0

At Y = 0 UY = 0 (Axial mode)

Representative Mesh Options

Target Solution and Results Comparison

Target Solution:

Freq = 208.333 Hz (Axial Mode)

Freq = 7.138 Hz (Bending Mode)

Results Comparison:

		1st Natural Frequency Ratio
Axial Mode
Shape	Angle	PLANE182	PLANE183	SOLID185	SOLID187	SOLID186
Rectangular	0	1.003	1.000	1.003	1.000	1.000
Trapezoidal	15	1.003	1.000	1.003	1.000	1.000
Trapezoidal	30	1.003	1.000	1.004	1.000	1.000
Trapezoidal	45	1.004	1.000	1.005	1.000	1.000
Parallelogram	15	1.003	1.000	1.003	1.000	1.000
Parallelogram	30	1.003	1.000	1.003	1.000	1.000
Parallelogram	45	1.003	1.000	1.003	1.000	1.000
Bending Mode
Rectangular	0	1.010	0.999	1.010	1.004	1.002
Trapezoidal	15	1.567	1.000	1.598	1.005	1.003
Trapezoidal	30	1.973	1.003	2.015	1.008	1.010
Trapezoidal	45	2.207	1.012	2.254	1.020	1.051
Parallelogram	15	1.040	0.999	1.043	1.005	1.002
Parallelogram	30	1.091	0.999	1.097	1.009	1.004
Parallelogram	45	1.119	0.999	1.127	1.020	1.010

Assumptions, Modeling Notes, and Solution Comments

The problem tests the influence of irregular element shapes on eigenvalue calculations. Although the problem appears rather simplistic in nature, it is a severe test for linear irregular shaped elements where accurate bending mode frequencies are required.
Since the beam is free of any constraints, only one-half of the beam is required for modeling. Symmetry constraints are applied at the mid-length of the models. To obtain the desired bending mode (in the XY plane) all nodes at Z = 0 are constrained in the Z direction. Additionally, for the axial mode only, all nodes at Y = 0 are constrained in the Y direction.
All load cases show good agreement in the prediction of the first axial natural frequency. This mode is simply linearly-varying longitudinal motion which is easily handled by both linear and quadratic elements. Irregular element shapes have only a minor effect on solution accuracy since axial motion is predominant.
For the linear elements (PLANE182, SOLID185), prediction of the first bending mode is significantly affected by irregularly shaped elements. If the elements are distorted, the stiffness of the element increases hence over predicting the bending mode natural frequency.
For the quadratic elements (PLANE183, SOLID186, SOLID187), prediction of the first bending mode is very good. Irregular element shapes for quadratic elements have little effect on the solution accuracy.