Benchmark C3

VMC3
Barrel Vault Roof Under Self Weight

Overview

Reference:

R. D. Cook, Concepts and Applications of Finite Element Analysis, 2nd Edition, John Wiley and Sons, Inc., 1981, pp. 284-287.

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Element Type(s):

4-Node Finite Strain Shell Elements (SHELL181)

8-Node Structural Shell Elements (SHELL281)

Input Listing:

vmc3.dat

Test Case

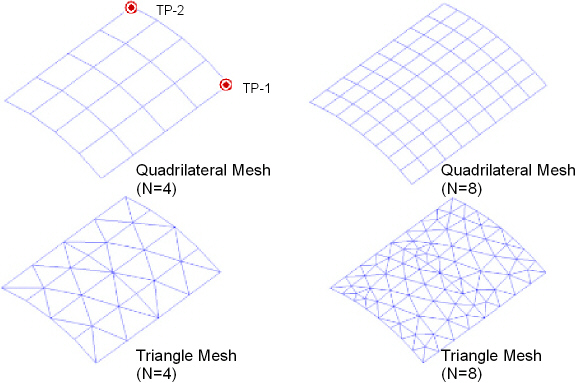
A cylindrical shell roof is subjected to gravity loading. The roof is supported by walls at each end and is free along the sides. Monitor the y displacement and bottom axial stress (σ_z) at target point 1, along with the bottom circumferential stress (σ_θ) at target point 2 for a series of test cases with increasing mesh refinement using quadrilateral and triangular element shapes. A companion problem that studies irregular element shapes is VMD2.

Figure 591: Barrel Vault Roof Problem Sketch

Material Properties

Geometric Properties

Loading and Boundary Conditions

E = 4.32 x 10⁸ N/m²

υ = 0.3

ρ = 36.7347 kg/m³

L = 50 m

R = 25 m

t = 0.25 m

Θ = 40°

g = 9.8 m/sec²

Parameter Definitions

N = No. elements along each edge

At x = 0 Symmetric

At z = 0 Symmetric

At x = L/2 UX = UY = ROTZ = 0

Figure 592: Representative Mesh Options

Target Solution

Target solution is obtained from an 8-node quadrilateral shell element solution with N=8, (see R. D. Cook, Concepts and Applications of Finite Element Analysis).

ETYP	N	DOF	UY(1), m	σ_z (1), Bottom	σ_θ (2), Bottom
--	8	2310	3016	358,420	-213,400

			Ratio
ETYP	N	DOF	UY(1)	σ_z (1), Bottom	σ_θ (2), Bottom
Results Comparison - Quadrilateral Elements
281	4	390	1.004	0.9536	1.027
281	8	1350	1.000	1.000	1.002
181	4	150	1.048	0.940	0.983
181	8	486	1.008	0.999	0.985
Results Comparison - Triangular Elements
281	4	774	0.971	0.953	0.980
281	8	2022	0.992	0.971	0.996
181	4	222	0.762	0.507	0.722
181	8	558	0.903	0.632	0.888

Assumptions, Modeling Notes, and Solution Comments

The problem is designed to test singly-curved shell elements under membrane and bending deformation. The quadrilateral mesh patterns produce uniform rectangular shapes while the triangle mesh patterns are as generated by the meshing algorithm in the solid modeler.
Results for SHELL181 in triangular form are presented, though they are not recommended for use. SHELL181 is based on a hybrid formulation for a quadrilateral element shape. Hence, degeneration of the element to a triangular shape will show some slight node-ordering dependence on the element solution.
The target solution is obtained in the prescribed reference for the author's 8-node shell element.
As expected, the quadratic SHELL281 performs better than the linear element SHELL181 for comparable meshes.
Results for the linear triangular-shaped elements is poor due to the constant-strain membrane behavior within the element. The effect of constant-strain membrane behavior is to overly stiffen the element under this type of loading, hence underpredicting both displacement and stresses. For triangular elements, only a fine mesh using the quadratic SHELL281 elements produces acceptable results.