Benchmark D1
VMD1
Straight Cantilever Beam Under Unit Load
Overview
Test Case
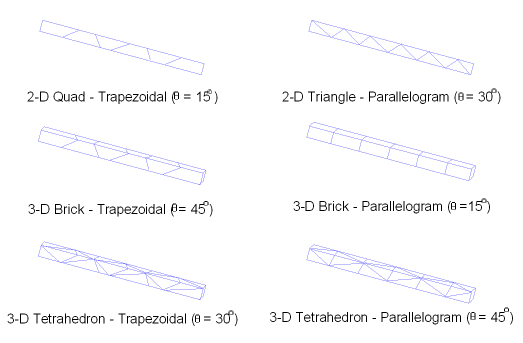
A straight cantilever beam, fixed at one end, is subjected to a unit load. Determine the displacement at the end of the beam for unit loads including extension, in-plane shear, out-of-plane shear, and twist (where applicable). Examine the influence of rectangular, trapezoidal, and parallelogram element shape models on tip displacement and the percent energy error norm.
| Material Properties | Geometric Properties | Loading | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
Results Comparison
| Tip Loading | Tip Displacement Ratio / % Error in Energy Norm | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shape/Direction | PLANE183 Triangular element | PLANE182 | PLANE183 | SOLID185 | SOLID187 | SOLID186 | ||||||
| Rectangular | ||||||||||||
| Extension | .997 | 6 | .996 | 0 | .999 | 5 | .988 | 0 | .993 | 11 | .994 | 3 |
| In-Plane Shear | .983 | 22 | .993 | 24 | 0.987 | 0 | .978 | 25 | .960 | 30 | .971 | 17 |
| Out-Of-Plane Shear | .973 | 27 | .959 | 33 | .961 | 22 | ||||||
| Twist | .892 | 10 | .910 | 24 | .903 | 8 | ||||||
| Trapezoidal (θ = 15°) | ||||||||||||
| Extension | .997 | 6 | .997 | 4 | .999 | 5 | .991 | 5 | .993 | 11 | .994 | 3 |
| In-Plane Shear | .982 | 23 | .293 | 66 | .986 | 7 | .272 | 66 | .959 | 31 | .969 | 18 |
| Out-Of-Plane Shear | .215 | 67 | .958 | 33 | .960 | 23 | ||||||
| Twist | .854 | 16 | .910 | 24 | .903 | 8 | ||||||
| Trapezoidal (θ = 30°) | ||||||||||||
| Extension | .997 | 6 | 0.999 | 4 | 1 | 4 | .993 | 6 | .993 | 11 | .994 | 3 |
| In-Plane Shear | .976 | 26 | 0.109 | 64 | .982 | 17 | .100 | 64 | .954 | 32 | .957 | 23 |
| Out-Of-Plane Shear | .072 | 64 | .954 | 34 | .954 | 25 | ||||||
| Twist | .742 | 27 | .910 | 25 | .903 | 8 | ||||||
| Trapezoidal (θ = 45°) | ||||||||||||
| Extension | .997 | 6 | 0.999 | 3 | 1.000 | 4 | .994 | 4 | .993 | 11 | .994 | 3 |
| In-Plane Shear | .961 | 32 | 0.052 | 59 | 0.967 | 36 | .047 | 59 | .939 | 37 | .891 | 34 |
| Out-Of-Plane Shear | .030 | 60 | .941 | 38 | .921 | 36 | ||||||
| Twist | .563 | 40 | .910 | 25 | .903 | 8 | ||||||
| Parallelogram (θ = 15°) | ||||||||||||
| Extension | .998 | 6 | .997 | 4 | .999 | 5 | .991 | 5 | .993 | 11 | .994 | 3 |
| In-Plane Shear | .983 | 22 | 0.812 | 38 | .988 | 1 | .798 | 40 | .959 | 31 | .971 | 18 |
| Out-Of-Plane Shear | .749 | 49 | .958 | 33 | .960 | 23 | ||||||
| Twist | .886 | 19 | .910 | 24 | .903 | 8 | ||||||
| Parallelogram (θ = 30°) | ||||||||||||
| Extension | .998 | 6 | .999 | 4 | .999 | 5 | .993 | 5 | .993 | 11 | .994 | 3 |
| In-Plane Shear | .980 | 24 | .680 | 51 | .991 | 4 | .669 | 53 | .954 | 33 | .972 | 21 |
| Out-Of-Plane Shear | .608 | 65 | .953 | 35 | .955 | 26 | ||||||
| Twist | .866 | 34 | .910 | 25 | .903 | 8 | ||||||
| Parallelogram (θ = 45°) | ||||||||||||
| Extension | .998 | 6 | 0.999 | 3 | 1.000 | 4 | .994 | 4 | .992 | 11 | .994 | 3 |
| In-Plane Shear | .970 | 29 | 0.632 | 55 | 0.997 | 8 | .624 | 57 | .940 | 38 | .968 | 27 |
| Out-Of-Plane Shear | .528 | 74 | .935 | 40 | .942 | 32 | ||||||
| Twist | .820 | 51 | .909 | 26 | .903 | 8 | ||||||
Assumptions, Modeling Notes, and Solution Comments
The straight cantilever beam is a frequently used test problem applicable to beam, plate, and solid elements. The problem tests elements under constant and linearly varying strain conditions. Although the problem appears rather simplistic in nature, it is a severe test for linear elements, especially when distorted element geometries are present.
The fixed boundary conditions at the left edge of the beam are not representative of a "patch test." Thus, under extensional loading, the finite element solution will not agree with the beam theory solution.
Element solution accuracy degrades as elements are distorted. The degradation is more pronounced for linear elements (PLANE182, SOLID185) than it is for quadratic elements (PLANE183, SOLID187, SOLID186). The degradation in performance for linear elements is most pronounced for bending loads coupled with irregular element shapes.
Distorted linear elements show more pronounced locking (excessive stiffness) for trapezoidal element shapes than for parallelogram shapes. Results clearly show under predicted displacements for trapezoidal element shapes for PLANE182 and SOLID185.
The quadratic elements show very good performance under all loadings and geometries. The good performance is attributed to the ability of the elements to properly handle bending and shear energy, in contrast to the linear elements.
The percent error in energy norm for each test case is displayed against the tip displacement ratio to illustrate the general correlation between the two for this particular problem. The linear elements show a patterned correlation between solution accuracy and the percent error in energy norm. For the quadratic elements the correlation pattern is similar. In both cases, the results illustrate that a considerable bandwidth on norm values may exist at any desired solution accuracy level for problems under a variety of load conditions with irregular element shapes.