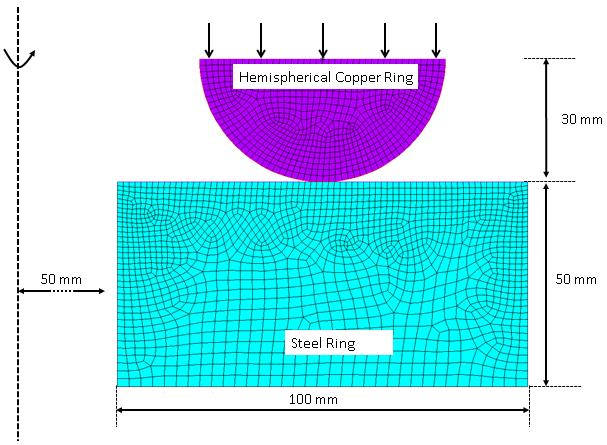
A 2D axisymmetric model representing the two rings is meshed and loaded as shown in the figure.
The rings are meshed with 2D axisymmetric PLANE182 elements (KEYOP(3) = 1). Frictionless contact is modeled between the two rings by overlaying the surfaces with contact elements (CONTA172) and target elements (TARGE169).
Two versions of this model are created, one with asymmetric contact and the other with symmetric contact. The first model uses asymmetric contact to simulate wear only on the top hemispherical ring; contact elements are defined on the top ring and target elements are defined on the bottom ring. In the second model, wear is simulated on both rings by defining symmetric contact between them; contact and target elements are defined on the surfaces of both rings.
Since wear can be modeled only on surfaces that have contact elements, the first example exhibits wear only on the hemispherical ring and the second example exhibits wear on both rings.
The (CONTA172) elements have the following settings:
Augmented Lagrangian formulation (KEYOPT(2) = 0, the default behavior)
Contact stiffness is updated at each iteration (KEYOPT(10) = 2)
Location of the contact detection point: nodal point, normal to target surface (KEYOPT(4) = 2)
Since simulating wear requires repositioning of the contact nodes, the contact detection point must be at nodes (KEYOPT(4) = 1 or 2), or projection-based contact can be used (KEYOPT(4) = 3).
Wear is simulated by defining a wear model (TB,WEAR) and
assigning it to the contact elements. You can specify a generalized form of the
Archard wear model as implemented in the program, or you can define your own wear
model via the userwear subroutine. Example input is provided
for both methods.
Contact elements must be defined on the surface undergoing wear. A wear model is then associated with those contact elements via a TB,WEAR material definition. The following command defines the Archard wear model:
TB,WEAR,MATID,,,ARCDwhere MATID is the material ID associated with the contact elements.
Simulating Wear via the Archard Wear Model
The Archard wear model is specified by inputting constants C1 through C4 (TBDATA). The constants represent the wear coefficient (K), material hardness (H), the contact pressure exponent (m), and the sliding velocity exponent (n).
The wear coefficient K can sometimes be scaled to simplify modeling. As an example, consider this ring-on-ring problem in which the rings are rotating at constant speed. The only effect of this rotation/sliding at the contact surface is to produce wear (friction is absent). The wear coefficient K can be scaled such that the rotation is not explicitly modeled, but its effect is included in the computation of wear. This greatly reduces the simulation time and effort.
More specifically, if a linear dependence of wear rate on the sliding velocity is assumed, the wear coefficient K can be scaled by the sliding velocity. In this example, sliding velocity is 2πN*R, where N = 100,000 revolutions/sec and R is the distance from the axis of rotation. Scaling K by 2πN*R results in the wear rate being linearly dependent upon the sliding velocity without explicitly modeling the sliding. The distance from the axis of rotation (R) is assumed to be constant for all points and is taken as 100 mm (the distance of the center of the ring from the axis of rotation).
To more accurately model the sliding velocity, you can program a user-defined wear
model (via the userwear subroutine) that includes sliding
velocity based on the distance from the axis of rotation.
Three example inputs are prepared to demonstrate different approaches to modeling wear:
Asymmetric contact is used to model wear in the hemispherical copper ring only. For this case, contact elements are defined on the copper ring while target elements are defined on the steel ring. The Archard wear model is defined as a material associated with the contact elements.
The material data for wear is defined via TBDATA commands. The wear properties for the copper ring are as follows:
| Wear Properties for the Copper Ring | ||
|---|---|---|
| Property | TBDATA Constant | Value |
| Wear Coefficient (K) | C1 | kcopper = 10e-13*2π1e5*100 (scaled by sliding velocity 2πN*R) |
| Hardness (H) | C2 | 1 MPa |
| Pressure exponent (n) | C3 | 1 |
| Velocity Exponent (m) | C4 | 0 |
To initiate wear after a steady state has been reached with respect to loading, TB,WEAR is used in conjunction with TBFIELD,TIME. The problem is simulated in two load steps. In the first load step, pressure is ramped to the desired level and wear is inactive during this load step. To achieve this TB,WEAR is defined as follows:
TB,WEAR,3,,,ARCD ! Mat #3 = material for wear of contact element on copper ring TBFIELD,TIME,0 ! Time at the beginning of load step 1 TBDATA,1,0,1,1,0,0 ! C1 = 0 results in no wear for load step 1 TBFIELD,TIME,1 ! Time at the end of load step 1 TBDATA,1,0,1,1,0,0 ! C1 = 0 results in no wear for load step 1
In the second load step, the pressure is held constant and wear is defined as follows:
TBFIELD,TIME,1.01 ! Time at the beginning of load step 2 TBDATA,1,kcopper,1,1,0,0 ! Value of wear coefficient resulting in initiation of wear TBFIELD,TIME,4 ! Time at the end of load step 2 TBDATA,1,kcopper,1,1,0,0 ! Wear coefficient kept constant during load step 2
To model wear in both rings, symmetric contact definitions are used with contact elements on both of the contacting rings, and wear properties for both the copper ring and the steel ring are defined.
The wear properties for the copper ring are as presented in the asymmetric example described above. The wear properties for the steel ring are as follows:
| Wear Properties for the Steel Ring | ||
|---|---|---|
| Property | TBDATA Constant | Value |
| Wear Coefficient (K) | C1 | ksteel = 1e-13*2π1e5*100 (scaled by sliding velocity 2πN*R) |
| Hardness (H) | C2 | 1 MPa |
| Pressure exponent (n) | C3 | 1 |
| Velocity Exponent (m) | C4 | 0 |
A symmetric contact definition between dissimilar meshes and materials can lead to a non-smooth contact pressure distribution. Thus, the option to use nodal stresses of the underlying solid element to calculate the wear increment (C5 = 1 on TBDATA) is recommended and is used in the symmetric example.
Wear for the copper ring is defined as in the asymmetric example with the addition of C5 = 1:
TB,WEAR,3,,,ARCD ! Mat #3 = material for wear of contact element on copper ring TBFIELD,TIME,0 ! Time at the beginning of load step 1 TBDATA,1,0,1,1,0,1 ! C1 = 0 results in no wear for load step 1; C5 = 1 = nodal stress TBFIELD,TIME,1 ! Time at the end of load step 1 TBDATA,1,0,1,1,0,1 ! C1 = 0 results in no wear for load step 1; C5 = 1 TBFIELD,TIME,1.01 ! Time at the beginning of load step 2 TBDATA,1,kcopper,1,1,0,1 ! Value of wear coefficient resulting in initiation of wear; C5 = 1 TBFIELD,TIME,7 ! Time at the end of load step 2 TBDATA,1,kcopper,1,1,0,1 ! Wear coefficient kept constant during load step 2; C5 = 1
Wear for the steel ring is defined as follows:
TB,WEAR,4,,,ARCD ! Mat #4 = material for wear of contact element on steel Ring TBFIELD,TIME, 0 ! Time at the beginning of load step 1 TBDATA,1,0,1,1,0,1 ! C1 = 0 results in no wear for load step 1; C5 = 1 = nodal stress TBFIELD,TIME,1 ! Time at the end of load step 1 TBDATA,1,0,1,1,0,1 ! C1 = 0 results in no wear for load step 1; C5 = 1 TBFIELD,TIME,1.01 ! Time at the beginning of load step 2 TBDATA,1,ksteel,1,1,0,1 ! Value of wear coefficient resulting in start of wear; C5 = 1 TBFIELD,TIME,4 ! Time at the end of load step 2 TBDATA,1,ksteel,1,1,0,1 ! Wear coefficient kept constant during load step 2; C5 = 1
The userwear subroutine is also demonstrated for this
problem and uses a model similar to the Archard wear model. In this example, the
input material data for userwear is similar to that of the
Archard model with the addition of angular speed being passed in.
The userwear subroutine uses five input properties
defined via TBDATA. C1 through C4 are the same as for the
Archard wear law, and C5 passes in the rotational speed (10,000 rotations/sec).
The example userwear subroutine calculates
position-dependent sliding velocity using the distance of the contact point from
the axis of rotation (R) and defines wear increment accordingly, therefore
avoiding explicit modeling of the sliding motion.
Asymmetric contact is considered in this example. The wear is defined as follows for the copper ring:
ang_velocity=2π1e5 ! angular velocity to be passed into userwear to calculate
! accurate sliding velocity
TB,WEAR,3,,5,USER ! Mat #3 = material for wear of contact element on copper ring
TBFIELD,TIME,0 ! Time at the beginning of load step 1
TBDATA,1,0,1,1,0,ang_velocity ! C1 = 0 results in no wear for load step 1
TBFIELD,TIME,1 ! Time at the end of load step 1
TBDATA,1,0,1,1,0, ang_velocity ! C1 = 0 results in no wear for load step 2
TBFIELD,TIME,1.01 ! Time at the beginning of load step 2
TBDATA,1,kcopper,1,1,0,ang_velocity ! Value of wear coefficient resulting in initiation of wear
TBFIELD,TIME,4 ! Time at the end of load step 2
TBDATA,1,kcopper,1,1,0, ang_velocity ! Wear coefficient kept constant during load step 2
Modeling wear involves repositioning contact surface nodes to simulate the material removal process. As a result, the element quality of the solid elements underlying the contact elements can quickly deteriorate. The examples show two ways of addressing this issue to enable simulating large amounts of wear.
Nonlinear Mesh Adaptivity
One way to improve the mesh is to use the nonlinear mesh adaptivity feature. A wear-based contact criterion triggers nonlinear mesh adaptivity whenever the mesh is distorted. The critical ratio between the amount of wear and the underlying solid element’s height is user-defined. When the criterion is reached, nonlinear mesh adaptivity is triggered.
Both the asymmetric example and the symmetric example use nonlinear mesh adaptivity, which requires the following steps:
Create a component that contains the contact elements that are undergoing wear.
Issue NLADAPTIVE to trigger adaptivity based on a wear criterion.
In both examples, the component name is “conreal”, and the following command triggers mesh adaptivity:
NLADAPTIVE,conwearel,add,contact,wear,0.50 ! Wear criterion is 50% of element height.
In this case adaptivity occurs whenever wear at any contact point exceeds 50% of the average height of the solid element underlying the contact element. Each time the criterion is reached, the analysis is stopped, the mesh quality is improved by morphing the mesh, history-dependent variables and boundary conditions are mapped, and the analysis is restarted with an improved mesh. This process is done automatically.
Manual Rezoning
Manual rezoning is another method that enables you to remesh the distorted mesh and continue the wear simulation with an improved mesh. This method, which requires more user intervention, is demonstrated in the user-defined wear example input file (see Input Files).