The following topics concerning the analysis and solution controls for this problem are available:
The common solution parameters used in all load steps of the analysis are as follows:
antype,static ! Static / quasi-static analysis type rescontrol,define,all,1 ! Restart files available at every substep nlgeom,on ! Allow large deformation eqslv,sparse ! Direct sparse solver outres,all,all ! Write out RST files for each substep
For each of the three load steps, specific solution controls are added, as follows:
Load Step 1:
time,1.0 ! analysis up to 1.0s nsubst,50,2000,50 ! initial, maximum and minimum number of ! substepsThe corresponding time step sizes are 0.02s, 5.0E-04s, and 0.02s, respectively. To ensure solution accuracy, the smallest time step is given.
Load Step 2:
time,2.0 ! analysis upto 2.0s deltim, 0.01, 1.e-05, 0.1 ! initial, minimum and maximum time step
Load Step 3:
time,3.0 ! analysis upto 3.0s deltim, 0.001, 1.e-05, 0.01 ! initial, minimum and maximum timestep
To minimize the possibility of convergence issues, the initial time step for load step 3 is the smallest. Convergence with fluid penetration loads is more difficult to achieve because, depending on the contact status, loaded contact surfaces may become unloaded and reloaded during solution.
The rezoning process itself has several steps which must be performed for a successful analysis. The most important steps relate to remeshing using the element-splitting method, as follows:
Determining the specific substep at which rezoning should be performed is a nontrivial, problem-dependent task.
Remeshing is usually necessary when the mesh becomes too distorted (when element angles approach 180 degrees). If old elements are too distorted at the rezoning step, however, mapping variables from the old mesh to a new mesh can be difficult. At extreme distortions, it is not possible to map new nodes at the corners of old elements accurately, affecting boundary condition mapping. This concern is critical in element splitting because old nodes are shared in new elements generated by splitting.
Element splitting does not change the mesh topology in the interior of the rezoned domain. The element angles before and after splitting remain the same, and the element aspect ratios remain the same; therefore, a badly shaped element cannot be improved by splitting alone. For best results, element splitting should occur a few substeps before the elements angles approach 180 degrees.
Mapping on state variables and residual equilibration can be difficult if the remeshing is done in the presence of very high stress/strain gradients. Remeshing should therefore be attempted at substeps where the gradients are not so high.
In general, the earlier remeshing is done in a load step, the more difficult it becomes for the problem to converge during restart. (It is also difficult to determine the correct rezoning region in the beginning of a loadstep, especially if it is the first loadstep.) Conversely, if remeshing occurs too late, the mapping may not succeed because the base mesh is already too distorted or large stress/strain gradients have developed.
For best results, attempt the first remeshing at a substep (S1) toward the later stages of a load step if that substep is not very close to divergence and where rezonable regions in the problem are clear. If successful, the solution can proceed; otherwise, attempt another remeshing at a different substep (S0) prior to S1, which reduces the element sizes by the time the remeshing at S1 can occur. This size reduction smooths out possible gradients and creates less element distortion by the time the solution reaches S1.
In this problem, the first rezoning is attempted first at load step 1, substep 20 (TIME = 0.4 s), which corresponds to substep S0. The next rezoning is done at load step 1, substep 50 (TIME = 0.8996 s) which corresponds to substep S1. If rezoning at S1 is attempted on its own, convergence does not improve (because at 0.8996 seconds, the seal bead already deforms to a large degree and creates mapping difficulties).
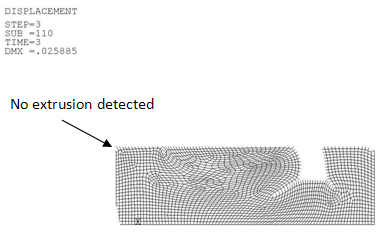
The focus of rezoning should be to perform the minimum number of remeshing steps possible while ensuring that the simulation results and the model mirror the actual physical problem behavior as closely as possible. It is possible that a nonlinear problem may converge without rezoning; however, the results may not be indicative of true physical behavior. For example, this seal problem was run without rezoning, producing the following results:
Because an extrusion gap is present and the problem is classified as a medium-to-low pressure seal, the extrusion is expected to occur. Without rezoning, a successful convergence in this case fails to provide a physically meaningful solution, as the mesh size is greater than the extrusion gap and therefore extrusion does not occur.
Using rezoning in the third load step (where fluid pressure is applied) causes convergence difficulties during remapping. Large shear-strain gradients develop near the extrusion due to the pressure differential caused by the fluid pressure. It is therefore necessary that remeshing occur before the fluid pressure is applied so that mapping does not occur when large strain gradients are present. To enable material flow in the extrusion gap, however, element sizes near the gap should be sufficiently small by the time the third load step is applied.
For this problem, optimal rezoning substeps occur in load steps 1 and 2. The magnitude of deformation in the seal bead is much larger in load step 1 (where the mating parts move) as opposed to load step 2 (a uniform temperature load). Because most of the deformation occurs in load step 1, remeshing is more critical there than in load step 2 (and two vertical rezonings in load step 1 are justified).
Load step 2 is a temperature load which expands the seal axially, thereby filling up most of the clearance gaps. The thermal expansion also contributes to the seal bead material being pushed through the extrusion gap. At least one local rezoning is required (around the extrusion) at load step 2 so that the incipient extrusion behavior can be modeled, and so the third and final rezoning is done in load step 2, substep 10 (TIME = 1.145s).
When a substep at which to remesh is identified, select the region(s) to be remeshed. The following remeshing topics are available:
The element-selection process for splitting can be done in any of the following ways:
Only solid elements are candidates for splitting. Contact and target elements are ignored.
If no elements are selected prior to mesh splitting (REMESH,SPLIT), all solid elements in the model are split and no transition elements are created.
Existing contact and target elements attached to base solid elements which have been split, and those which have been replaced by smaller transition elements, are automatically deleted.
Two methods for remeshing using element splitting are available:
Create all quad transitions between split and unsplit elements:
REMESH,SPLIT
or
REMESH, SPLIT,,,,TRAN,QUAD
Create degenerate (triangular) transitions between split and unsplit elements:
REMESH,SPLIT,,,,TRAN,DEGE
An all-quad transition is usually more than a single element layer deep. It is topologically difficult to resolve nodal incompatibilities from the split to the unsplit elements in a single-element layer, especially in an unstructured quad mesh.
Using degenerate transitions between the split and unsplit elements usually resolves nodal incompatibilities in a single element layer. Triangular elements tend to lock, however.
Provided that the transition elements are not too distorted and do not overlay other transition elements, it is preferable to use an all-quad transition for nonlinear problems. The degenerate transition is useful in cases where the quad transitions become too distorted or where the problem is not bending- or compression-dominated. In this problem, an all-quad transition is used to prevent volumetric locking. With nested splitting schemes, it is possible to prevent the all-quad transition regions from intersecting.
Relative size control of split elements is of prime importance to remeshing by element splitting.
The splitting operation subdivides a quad element into four quad elements, a triangular element into four triangular elements, and a degenerate element into three quadratic elements. After one cycle of splitting a quad base element, therefore, the split elements are 1/4 the area of the base element.
If N such splittings occur, the final split elements have an area of (1/4)N of that of the base element. If multiple horizontal rezonings overlap or multiple vertical rezonings are done on the same region, it becomes increasingly difficult to generate proper transitions due to the increasing size disparity of the split and unsplit elements.
One method for overcoming the size disparity between split and unsplit elements is to design a nesting scheme for splitting during vertical rezoning. The nesting should allow the Nth remeshing region to be sufficiently larger than the (N+1)th remeshing so that the transitions between the two regions do not overlap.
Using such nesting schemes, it is possible to design mesh grading from coarse to fine, improving solution performance. In this problem, the nesting scheme allows the remeshed regions in the first, second, and third rezonings to be successively reduced while overlapping, therefore creating a good gradation of the mesh.
Nesting schemes can also alleviate the effect of large tensile strains on element splitting strategies, where aspect ratios of split elements can be adversely affected.
After remeshing (REMESH,FINI), corresponding new contact and target elements which respect the topology of the split solid elements are generated automatically for the meshed region. Isolated rigid target elements (as done in the modeling of the moving mating part) cannot be remeshed and persist throughout the life cycle of the analysis.
At this stage, it is necessary to map boundary conditions, loads, and temperatures from the old mesh to the new mesh.
The MAPSOLVE command maps the state variables from the old mesh to the new mesh and balances the residuals by modifying the displaced state of the new mesh. The presence of large stress or strain gradients in the old mesh may cause nonconvergence of the residuals in the new mesh. View the result plot to determine if the mesh substep can be split depending on the presence of stress/strain gradients.
Convergence problems during mapping can also occur if a very large size difference exists between the elements of the old and new meshes. Regions are allowed to overlap during horizontal splitting operations, so it is possible to generate an arbitrarily small element size if many such regions overlap (given that the new element area after N such overlapped horizontal splitting operations is (1/4)N of the old element size). Nesting the remeshed regions can alleviate this problem.
In most cases, convergence difficulties during mapping also indicate convergence difficulties during the analysis restart. It is therefore good practice to remesh a few substeps earlier (if possible) if MAPSOLVE requires a large number of bisections to converge.
|
The Degree of Element Deformation Affects Mapping For contact-element generation and remapping, the program attempts to detect a new node (of a split element) in an old element. Because element splitting retains the nodes of the old element in the new elements, the algorithm often involves detecting a new node at the corner of an old element. Element splitting also retains the element angular values, so for badly skewed elements, it is difficult to map a corner node of a new element to the corresponding parent element. This mapping difficulty can cause the creation of new contact elements to fail, and boundary conditions may not be properly generated for the new mesh. It is therefore important to perform element splitting before the element becomes too badly skewed. The guidelines used to select the substep and region for splitting also apply when considering how base element skewness may affect contact- and boundary-condition generation. |
After mapping quantities from the old to the new mesh and rebalancing the residual forces, a multiframe restart (ANTYPE,,RESTART,,,CONTINUE) resumes the nonlinear solution with the new mesh.
It is possible to readjust the number of substeps at this stage to improve convergence.