From a macroscopic perspective, the phase-transformation mechanisms involved in superelastic behavior are:

Figure 4.57: Typical Superelasticity Behavior

Two of the phase transformations are considered here: A->S and S->A. The material is composed of two phases, the austenite (A) and the martensite (S). Two internal variables, the martensite fraction (ξ_S) and the austenite fraction (ξ_A), are introduced. One of them is a dependent variable, and they are assumed to satisfy the relation expressed as:

The independent internal variable chosen here is ξ_S.

The material behavior is assumed to be isotropic. The pressure dependency of the phase transformation is modeled by introducing the Drucker-Prager loading function, as follows:

where α is the material parameter, σ is the stress, and 1 is the identity tensor.

The evolution of the martensite fraction, ξ_S, is then defined as follows:

where:

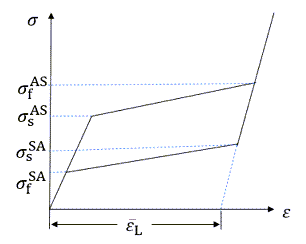
where are the material parameters shown in the following figure:

Figure 4.58: Idealized Stress-Strain Diagram of Superelastic Behavior

where are the material parameters shown in Figure 4.58: Idealized Stress-Strain Diagram of Superelastic Behavior.

The material parameter α characterizes the material response in tension and compression. If tensile and compressive behaviors are the same, then α = 0. For a uniaxial tension-compression test, α can be related to the initial value of austenite to martensite phase transformation in tension and compression (, respectively) as:

The stress-strain relation is:

where D is the elastic stiffness tensor, is the transformation strain tensor, and is the material parameter shown in Figure 4.58: Idealized Stress-Strain Diagram of Superelastic Behavior.

To model the difference between the austenite and martensite elastic properties, the elastic modulus (used in the material constitutive model) is a function of the martensite fraction , the elastic modulus of pure austenite (the initial input elastic modulus), and the elastic modulus of pure martensite :

To model the superelastic behavior of shape memory alloys, initialize the data table via the TB,SMA command's SUPE option.

Define the elastic behavior in the austenite state (MP).

The superelastic SMA option is described by six constants that define the stress-strain behavior in loading and unloading for the uniaxial stress-state.

For each data set, define the temperature (TBTEMP), then define constants C1 through C7 (TBDATA). You can define up to 99 sets of temperature-dependent constants in the same way.

Table 4.30: Superelastic Option Constants

Constant	Meaning	Property
C1		Starting stress value for the forward phase transformation
C2		Final stress value for the forward phase transformation
C3		Starting stress value for the reverse phase transformation
C4		Final stress value for the reverse phase transformation
C5		Maximum residual strain
C6	α	Parameter measuring the difference between material responses in tension and compression
C7		Elastic modulus of the full martensite phase If 0 or undefined, the martensite and austenite phases share the same elastic modulus

MP,EX,1,60000.0
MP,NUXY,1,0.36
Define SMA material properties
TB,SMA,1,,,SUPE
TBDATA,1, 520, 600, 300, 200, 0.07, 0.0

The shape memory effect was based on a 3D thermomechanical model for stress-induced solid phase transformations that was presented in [2] [3][4]. Within the framework of classical irreversible thermodynamics, the model is able to reproduce all of the primary features relative to shape memory materials in a 3D stress state. The free energy potential is set to:

where:

D = material elastic stiffness tensor

= total strain

= total transformation strain

= deviatoric transformation strain

τM(T) = a positive and monotonically increasing function of the temperature as 〈β(T - T0)〉+ in which 〈∙〉+ is the positive part of the argument (also known as Maxwell stress).

β = material parameter

T = temperature

T0 = phase-balance temperature

h = material parameter related to the hardening of the material during the phase transformation

= indicator function introduced to satisfy the constraint on the transformation norm [1] in which

from which we have

where X _tr is defined as the transformation stress.

Stresses, strains, and the transformation strains are then related as follows:

Splitting the stress into deviatoric and volumetric components, we have

where S is the deviatoric stress and p is the volumetric stress (also called hydrostatic pressure)

The transformation stress is given as follows:

where γ is defined by

where is a maximum value of .

Numerous experimental tests show an asymmetric behavior of SMA in tension and compression, and suggest describing SMA as an isotropic material with a Prager-Lode-type limit surface. Accordingly, the following yield function is assumed:

where X _tr is the transformation stress, J₂ and J₃ are the second and third invariants of transformation stress, m is a material parameter related to Lode dependency, and R is the elastic domain radius.

J₂ and J₃ are defined as follows:

The evolution of transformation strain is defined as:

where ξ is an internal variable and is called as transformation strain multiplier. ξ and F(X _tr) must satisfy the classical Kuhn-Tucker conditions, as follows:

which also reduces the problem to a constrained optimization problem.

The elastic properties of austenite and martensite phase differ. During the transformation phase, the elastic stiffness tensor of material varies with the deformation. The elastic stiffness tensor is therefore assumed to be a function of the transformation strain , defined as:

where D _A is the elastic stiffness tensor of austenite phase, and D _S is the elastic stiffness tensor of martensite phase. The Poisson’s ratio of the austenite phase is assumed to be the same as the martensite phase. When the material is in its austenite phase, D = D _A, and when the material undergoes full transformation (martensite phase), D = D _S.

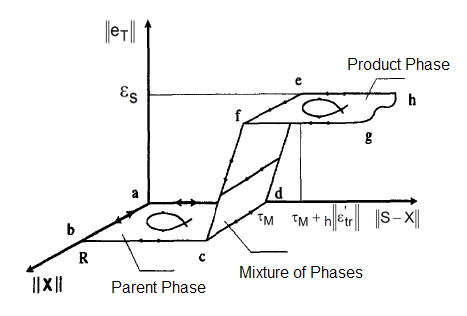
The following figure illustrates a number of the mechanical model features:

Figure 4.59: Admissible Paths for Elastic Behavior and Phase Transformations

The austenite phase is associated with the horizontal region abcd. Mixtures of phases are related to the surface cdef. The martensite phase is represented by the horizontal region efgh. Point c corresponds to the nucleation of the martensite phase. Phase transformations take place only along line cf, where . Saturated phase transformations are represented by paths on line fg. The horizontal region efgh contains elastic processes except, of course, those on line fg.

A backward Euler integration scheme is used to solve the stress update and the consistent tangent stiffness matrix required by the finite element solution for obtaining a robust nonlinear solution. Because the material tangent stiffness matrix is generally unsymmetric, use the unsymmetric Newton-Raphson option (NROPT,UNSYM) to avoid convergence problems.

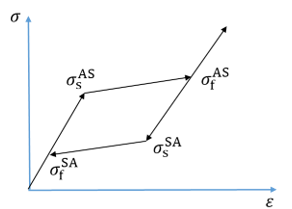
Assuming that A and S share the same elastic modulus (D_S = D_A) in a uniaxial loading under the constant temperature T, these are the four critical stress points (shown in Figure 4.60: Stress Points at the Start/End of the Phase Transfers) at the start and end of the phase transformations:

Figure 4.60: Stress Points at the Start/End of the Phase Transfers

To model the shape memory effect behavior of shape memory alloys, initialize the data table via the TB,SMA command’s MEFF option.

Define the elastic behavior in the austenite state (MP).

The shape memory effect option is described by seven constants that define the stress-strain behavior of material in loading and unloading cycles for the uniaxial stress-state and thermal loading.

For each data set, define the temperature (TBTEMP), then define constants C1 through C7 (TBDATA). You can define up to 99 sets of temperature-dependent constants in this manner.

MP,EX,1,60000.0
MP,NUXY,1,0.36
Define SMA material properties
TB,SMA,1,,,MEFF
TBDATA,1,1000, 223, 50, 2.1, 0.04, 45000
TBDATA,7,0.05

The isotropic elastic behavior in the austenite state is defined via the material elastic constants (MP or TB).

To define the constants, initialize the data table (TB,SMA) with options (TBOPT) METE, METL, METH, MEPD, and METC. The function of each option follows:

METE (required) -- Defines the elastic phase dependent response and thermal expansion.

METL (required) -- Specifies the limits of transformation in strain-stress-temperature space and thus defines the phase diagram of a given SMA material.

METH (required) -- Considers the smooth behavior of transformation by applying a hardening function for the evolution of the martensite volume fraction .

MEPD (required) -- Defines the plastic phase-dependent yielding response. The plasticity exhibits linear kinematic and nonlinear isotropic hardening:

METC (optional) -- Defines the tension-compression asymmetry response and hysteresis response. If not defined, the program determines default parameter values.

For each data set, define temperature- and field-dependence (TBFIELD), if any, then define the material parameters (TBDATA) as shown in the following tables:

Table 4.32: TBDATA Constants for TB,SMA,,,,TBOPT = METE

Constant	Meaning	Property	Range
C1		Young’s modulus of martensite
C2		Thermal expansion coefficient

Table 4.33: TBDATA Constants for TB,SMA,,,,TBOPT = METL

Constant	Meaning	Property	Range
C1		Maximum transformation strain
C2		Phase-transformation limit
C3		Phase-balance temperature
C4		Entropy difference for forward transformation
C5		Entropy difference for reverse transformation

Table 4.34: TBDATA Constants for TB,SMA,,,,TBOPT = METH

Constant	Meaning	Property	Range
C1		Transformation hardening modulus
C2		Transformation hardening factor
C3		Transformation hardening factor
C4		Transformation hardening factor
C5		Transformation hardening exponent
C6		Transformation hardening exponent

Table 4.35: TBDATA Constants for TB,SMA,,,,TBOPT = MEPD

Constant	Meaning	Property	Range
C1		Isotropic hardening modulus of austenite
C2		Isotropic hardening modulus of martensite
C3		Plastic yield point of austenite
C4		Isotropic plastic yield saturation point of austenite
C5		Plastic yield point of martensite
C6		Isotropic plastic yield saturation point of martensite
C7		Isotropic plastic yield saturation rate parameter
C8		Kinematic hardening modulus

Table 4.36: TBDATA Constants for TB,SMA,,,,TBOPT = METC

Constant	Meaning	Property	Range	Default
C1		Young’s modulus of martensite in compression
C2		Maximum transformation strain in compression
C3		Compression plasticity factor (the ratio of the compression-yield point to the tension-yield point)		1
C4		Hardening internal loop factor		0
C5		Hysteresis internal loop factor		0

!================================================!
! Material parameters for SMA plasticity model
!================================================!
! Thermo-elasticity
C1 = 32575      !EA
C2 = 29246      !ES
C3 = 0.33       !nu
C4 = 0.00001    !alpha
! Transformation limits
C5 = 0.039      !eL
C6 = 79.2       !YS
C7 = 259.57     !theta0
C8 = 5.16       !deletaf
C9= 3.98        !deletar
! Transformation hardening
C10= 1900       !mut
C11= -100       !a1
C12= 300        !a2
C13= 0.0        !a3
C14= 10.0       !n1
C15= 10.0       !n2
! Plasticity
C16= 5000       !mupA
C17= 5000       !mupS
C18= 30         !YpA
C29= 1000       !YpS
C20= 30         !YmA
C21= 1200       !YmS
C22= 1600       !CH
C23=0           !mup

MPTEMP,,,,,,,,
MPTEMP,1,270
MPDATA,EX,1,,C1
MPDATA,PRXY,1,,C3
TB,SMA,mat1,1,4,METE
TBDATA,1,C2, C4
TB, SMA,mat1,1,5,METL
TBDATA,1,C5,C6,C7,C8,C9
TB,SMA,mat1,1,6,METH
TBDATA,1,C10,C11,C12,C13,C14,C15
tb,sma,mat1,1,8,MEPD
tbdata,1,C16,C17,C18,C19,C20,C21
tbdata,7,C22,C23

 

4.15.1.3.1.1. Specifying Temperature Units

The default temperature unit is Kelvin. If using another temperature unit, the corresponding coefficients for the constants need to be converted. This table shows how to convert a given coefficient value from one temperature-unit system to another:

Table 4.37: Example: Converting Coefficient Values

Constant	Kelvin (Default)	Celsius	Farenheit