The following examples are available:
This example problem demonstrates the calculation of the transient magnetic field in a copper block placed between the pole-pieces of a C-magnet subject to a sinusoidal current excitation. A similar magnetic circuit is described in P.P. Silvester and R.L. Ferrari "Finite Elements for Electrical Engineers" (Third edition), Cambridge University Press (1996), pp. 365-367. In the present example, magnetic circuit parameters have been chosen arbitrarily and the simulation results differ from those in the reference.
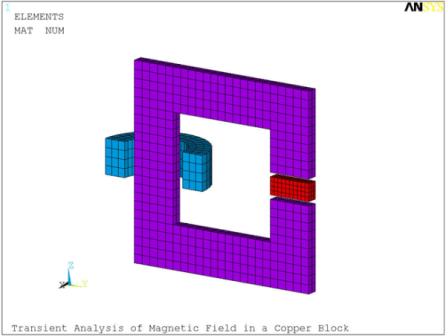
A 2.5 x 5 x 2 cm copper block with electric resistivity ρ = 1.7e-7 Ωm is placed between the pole-pieces of a C-magnet. The magnet consists of a 2.5 cm thick C-shaped iron core with relative permeability μ = 1000 and a 4 cm long cylindrical coil with an average radius of 5 cm carrying a 50 Hz sinusoidal current. The problem considers a half symmetry model of the electromagnet and the block (Figure 8.1: Finite Element Model of the C-Magnet and the Conducting Block) which also includes a 10 cm thick layer of surrounding air.
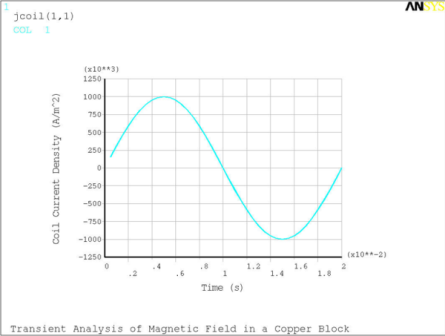
Element SOLID236 is used for all parts of the model. The conducting block is modeled using the electromagnetic analysis option (KEYOPT(1)=1) with time-integrated electric potential (KEYOPT(2)=2). The coil is modeled as a stranded conductor (KEYOPT(1)=0) with a sinusoidal current density (Figure 8.2: Current Density in the Coil) applied as a tabular JS-body load (BFV,,JS,,%jcoil%) with time as a primary variable. The same magnetic analysis option (KEYOPT(1)=0) is used to discretize the iron core (bricks) and the air (tetrahedra).
Flux parallel magnetic boundary conditions (AZ = 0) are imposed on the exterior surfaces of the domain and on the symmetry plane. Zero potential (VOLT = 0) electric boundary conditions are applied on the symmetry plane of the conducting block.
A transient electromagnetic analysis is performed during one full cycle T (T = 0.02 s) to determine the magnetic field in the conducting block. Note that to minimize the size of the output files, only the element results for the element component CCB that includes the coil, core and the block (OUTRES,ESOL,,CCB) are stored.
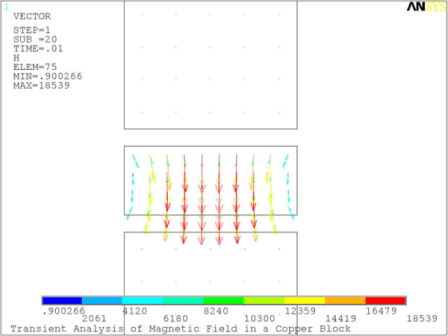
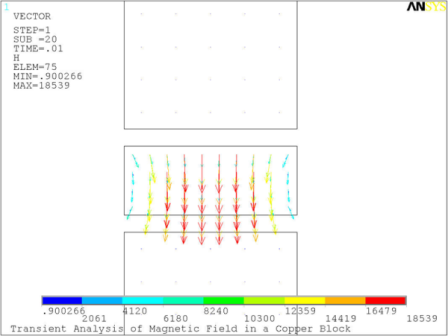
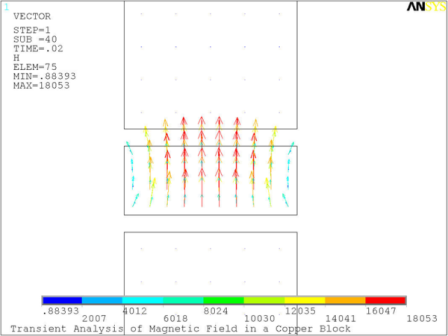
The progression of the magnetic field through the copper block is shown in Figure 8.3: Magnetic Field in the Copper Block at Successive Time Intervals at five successive time intervals T/40, T/4, T/2, 3T/4, and T.
Figure 8.4: Eddy Currents in the Conducting Block shows the eddy currents distribution in the block at the end of the cycle.
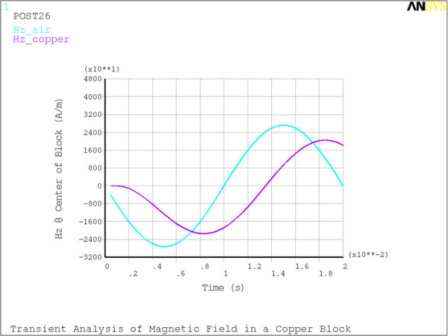
Figure 8.5: Magnetic Field between the Pole-Pieces with and without the Copper Block shows the magnetic field H at the center-point between the pole-pieces in the C-magnet with the copper block in place and without it. The figure demonstrates that the field inside the copper block is attenuated and lagging in phase compared to the external magnetic field.
/title, Transient Analysis of Magnetic Field in a Copper Block /VUP,1,z /VIEW,1,3,2,1 /PNU,mat,1 /NUM,1 ! *** Problem Parameters pi=acos(-1) muo=pi*4e-7 ! --- Geometry a=0.05 ! core and copper block cross section edge length, m b=0.1 ! distance between inner surfaces of magnetic circuit, m c=0.02 ! copper block thickness, m gap=0.005 ! pole face/copper block gap,m r=0.05 ! coil average radius, m l=0.04 ! coil length, m ac=0.025 ! coil cross section edge length, m dext=0.1 ! extent of domain beyond modeled components, m esz1=0.005 ! element size of conductive block esz2=0.01 ! element size of core and coil esz3=0.05 ! mesh size of surrounding domain ! --- Material properties muc=1000 ! core relative permeability mub=1 ! conducting block relative permeability rho=1.7e-8 ! electric resistivity of copper (Ohm-m) ! --- Excitation parameters J=1e6 ! coil current density amplitude (A/m^2) ncyc=1.0 ! number of cycles nsubT=40 ! number of time steps per cycle f=50 ! frequency, Hz ! --- Derived parameters skin=sqrt(rho/(pi*mub*muo*f)) ! skin depth T=1/f ! time period tend=ncyc*T ! solution time nsubs=nsubT*ncyc ! total number of time steps ! table array - sin current vs. time *dim,jcoil,table,nsubs *do,i,1,nsubs jcoil(i,1)=J*sin(2*pi*f*(i/nsubs)*T) jcoil(i,0)=(i/nsubT)*T *enddo /axl,x,Time (s) /axl,y,Coil Current Density (A/m^2) *vplo,jcoil(1,0),jcoil(1,1) /com, /com, *** BLOCK EDGE LENGTH = %a% m, SKIN DEPTH = %skin% m /com, /nopr ! *** FE Model /PREP7 ! --- Core vsel,none block,0,-a/4, -a/2,a/2, -b/2-5*a/4,b/2+5*a/4 block,0,-a/4, -a/2,2*a+b, -b/2-5*a/4,-b/2-a/4 block,0,-a/4, -a/2,2*a+b, b/2+a/4,b/2+5*a/4 block,0,-a/4, a+b,2*a+b, -b/2-5*a/4,-(gap+c/2) block,0,-a/4, a+b,2*a+b, gap+c/2,b/2+5*a/4 vovl,all vatt,2,2,2 ! --- Conducting block vsel,none block,0,-a/4, a+b,2*a+b, -c/2,c/2 vatt,3,3,3 ! --- Coil vsel,none cyli,r-ac/2,r+ac/2, -l/2,l/2, 90,180 cyli,r-ac/2,r+ac/2, -l/2,l/2, 180,270 allsel,belo,volu numm,kp vatt,4,4,4,14 allsel cm,keep_v,volu ! --- Air box *get,xmin,kp,,mnloc,x *get,ymin,kp,,mnloc,y *get,ymax,kp,,mxloc,y *get,zmin,kp,,mnloc,z *get,zmax,kp,,mxloc,z vsel,none block,xmin-dext,0, ymin-dext,ymax+dext, zmin-dext,zmax+dext cm,scrap_v,volu allsel vsbv,scrap_v,keep_v,,dele,keep cmse,u,keep_v cm,air_v,volu vatt,1,1,1 allsel ! --- Air et,1,236 ! AZ mp,murx,1,1 ! --- Core et,2,236 ! AZ mp,murx,2,muc ! --- Conducting block et,3,236,1,2 ! AZ + time-integrated VOLT mp,murx,3,mub mp,rsvx,3,rho ! --- Coil et,4,236 ! AZ mp,murx,4,1 cswp,14,1 ! cylindrical ESYS for coil current direction csys vsel,s,mat,,3 ! brick mesh for the block esize,esz1 vmesh,all vsel,s,mat,,2,4,2 ! brick mesh for the coil and core esize,esz2 vmesh,all vsel,s,mat,,1 ! mesh air box (hex-to-tet) esize,esz3 mshape,1 vmes,all allsel eplo ! Define Coil-Core-Block element component esel,s,type,,2,4 cm,CCB,elem eplo allsel ! *** Boundary Conditions and Loads asel,s,ext da,all,az ! flux parallel magnetic BCs vsel,s,mat,,3 allsel,belo,volu asel,r,loc,x da,all,volt ! current normal to symmetry plane vsel,s,mat,,4 bfv,all,js,0,%jcoil%,0 ! tabular current density load allsel fini ! *** SOLVE /SOLU antype,trans time,tend nsub,nsubs outres,esol,all,CCB kbc,1 ! step applied load solve fini ! *** POST PROCESS /POST1 !set,,,,,0 ! results at time=0 s !set,,,,,T/4 ! results at time=T/4 s !set,,,,,T/2 ! results at time=T/2 s !set,,,,,3*T/4 ! results at time=3*T/4 s set,last,last cmsel,s,CCB ! select coil, core and conducting block plve,h,,,,vect,,on ! plot magnetic field esel,s,mat,,3 ! select conducting block plve,jt,,,,vect,,on ! plot current density allsel fini *dim,Hz,array,nsubs /post26 ansol,2,node(0,3*a/2+b,0),h,z,Hz_copper /axl,x,Time (s) /axl,y,Hz @ Center of Block (A/m) plva,2 vget,Hz,2 fini /PREP7 et,3,236 ! replace copper block by an 'air' block fini ! *** Repeat solution /SOLU antype,trans time,tend nsub,nsubs outres,esol,all,CCB kbc,1 ! step applied load solve fini /POST26 ansol,2,node(0,3*a/2+b,0),h,z,Hz_air /axl,x,Time (s) /axl,y,Hz @ Center of Block (A/m) vput,Hz,3,,,Hz_copper plvar,2,3 fini
Another Ansys, Inc. publication, the Mechanical APDL Verification Manual, contains other examples of various types of analyses, including the following 3D transient edge-based magnetic analysis example:
VM121 -- Voltage Forced Coil (1/8 Symmetry)