Problem Description
A rectangular beam with perforated holes under transverse motion is modeled to compute the effective damping and squeeze stiffness coefficients. The thin film surface of the structure is modeled with FLUID136 elements. FLUID138 elements are used to model the hole regions. By altering the boundary condition of the free FLUID138 node, we can simulate different pressure boundary conditions of the hole region. The purpose of the analysis is to compute the equivalent squeeze stiffness and damping coefficient for an assumed uniform plate velocity. A harmonic analysis is performed at 150 kHz. A previous modal analysis indicated that the pertinent eigenfrequency was 150 kHz. Since the analysis is linear, the magnitude of the velocity can be arbitrary for computing the coefficients.
Three cases were considered:
Holes modeled with no resistance (pressure = 0 at hole location, no FLUID138 elements ).
Holes modeled with finite resistance (FLUID138 elements modeled, pressure set to zero on fluid node at top of plate).
Holes modeled with infinite resistance (no pressure specification at hole location, no FLUID138 elements).
Case 1 is typical for large diameter holes compared to the hole depth. Case 3 is typical for very high flow resistance, which happens in the case of narrow and long holes. Case 2 is the most accurate case where the fluid pressure drop is taken into account by the FLUID138 elements.
Results
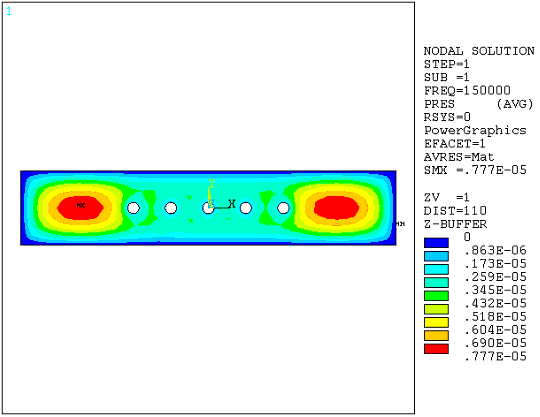
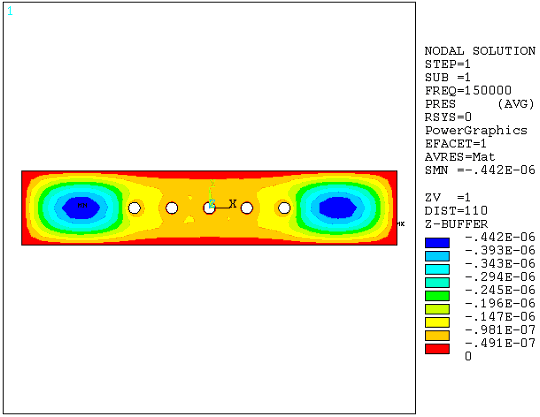
Table 3.2: Beam Model Results Considering Perforated Holes lists the damping and squeeze coefficient results. Figure 3.6: Pressure Distribution (Real Component) and Figure 3.7: Pressure Distribution (Imaginary Component) illustrate the real and imaginary pressure distribution. The input file for case 2 is listed.
Table 3.2: Beam Model Results Considering Perforated Holes
| Frequency (kHz.) | Hole option | Damping Coefficient | Squeeze stiffness coefficient |
|---|---|---|---|
| 150 | Infinite resistance | 2.016e-5 | 1.201 |
| 150 | Finite resistance | 1.325e-5 | .5465 |
| 150 | No resistance | 1.165e-5 | .4607 |
Command Listing
The input file for this example is shown below for the finite-resistance Case 2
/batch,list /PREP7 /title, Damping and Squeeze film stiffness calculations for a rigid /com, plate with holes /com uMKS units ET, 1,136,1 ! 4-node option, High Knudsen Number ET, 2,138,1 ! Circular hole option, High Knudsen Number s_l=100 ! Half Plate length (um) s_l1=60 ! Plate hole location s_w=20 ! Plate width s_t=1 ! Plate thickness c_r=3 ! Hole radius d_el=2 ! Gap pamb=.1 ! ambient pressure (MPa) visc=18.3e-12 ! viscosity kg/(um)(s) velo=2000 ! arbitrary velocity (um/s) freq=150000 ! Frequency (Hz.) pi=3.14159 omega=2*pi*freq ! Frequency (rad/sec) pref=.1 ! Reference pressure (MPa) mfp=64e-3 ! mean free path (um) Knud=mfp/d_el ! Knudsen number mp,visc,1,visc ! Dynamic viscosity gap mp,visc,2,visc ! Dynamic viscosity holes r,1,d_el,,,pamb ! Real constants - gap rmore,pref,mfp r,2,c_r,,,pamb ! Real constants - hole rmore,pref,mfp ! Build the model rectng,-s_l,s_l,-s_w,s_w ! Plate domain pcirc,c_r ! Hole domain agen,3,2,,,-s_l1/3 agen,3,2,,,s_l1/3 ASBA, 1, all TYPE, 1 MAT, 1 smrtsize,4 AMESH, all ! Mesh plate domain ! Begin Hole generation *do,i,1,5 nsel,all *GET, numb, node, , num, max ! Create nodes for link elements N, numb+1,-s_l1+i*s_l1/3,, N, numb+2,-s_l1+i*s_l1/3,, s_t TYPE,2 MAT, 2 REAL,2 NSEL, all E, numb+1, numb+2 ! Define 2D link element ESEL, s, type,,1 NSLE,s,1 local,11,1,-s_l1+i*s_l1/3 csys,11 NSEL,r, loc, x, c_r ! Select all nodes on the hole circumference NSEL,a, node, ,numb+1 *GET, next, node, , num, min CP, i, pres, numb+1, next nsel,u,node, ,numb+1 nsel,u,node, ,next CP, i, pres,all !Coupled DOF set for constant pressure csys,0 *enddo ! End hole generation nsel,s,loc,x,-s_l nsel,a,loc,x,s_l nsel,a,loc,y,-s_w nsel,a,loc,y,s_w nsel,r,loc,z,-1e-9,1e-9 d,all,pres ! Fix pressure at outer plate boundary nsel,all esel,s,type,,2 nsle,s,1 nsel,r,loc,z,s_t d,all,pres,0 ! P=0 at top of plate dlist,all allsel bfe,all,flue,,velo ! Apply arbitrary velocity fini finish /solu antyp,harm ! Full Harmonic analysis harfrq,freq solve finish /post1 esel,s,type,,1 set,1,1 etable,presR,pres ! extract "Real" pressure etable,earea,volu smult,forR,presR,earea ! compute "Real" force ssum *get,Fre,ssum,,item,forR set,1,1,,1 etable,presI,pres ! extract "Imaginary" pressure smult,forI,presI,earea ! compute "Imaginary" pressure ssum *get,Fim,ssum,,item,forI K=abs(Fim*omega/velo) ! Compute equivalent stiffness C=abs(Fre/velo) ! Compute equivalent damping /com, ******* Equivalent stiffness ************************ *stat,K /com, ******* Equivalent damping ************************** *stat,C finish