This example problem uses the FLUID220 element to demonstrate acoustic propagation in a lined guide with the complex impedance boundary and mean flow.
The lined duct with the dimension 4x1x0.075 m3 is terminated by Perfectly matched layers (PML) in the acoustic propagating direction.
The impedance boundary with the complex impedance Z = 417.45+j417.45 ohms is applied on the top boundary of the duct. The bottom boundary is set to the rigid wall.
The volume mass source is located at the center of the duct to model a monopole source with radius = 0.2 m. The nodal mass source is set to q=1/ω (ω is the angular frequency).
The uniform mean flow with Mach number = 0.3 in the x-direction is investigated. The working frequency is 384.36 Hz.
The acoustic domain is the air with mass density = 1.21 kg/m3 and sound speed = 345 m/s. It is necessary to use PML to truncate the duct, rather than the matched impedance boundary, since multiple modes may be excited in the model.
/batch,list /nopr /prep7 pi=acos(-1.) c0=345 ! sound speed in the air rho=1.21 ! the air mass density mach=0.3 ! Mach number v0=mach*c0 ! mean flow velocity k=7 ! working wave number freq=k*345/(2*pi) ! working frequency wavelen=c0/freq ! wave length h=wavelen/12 ! mesh size d=2 ! half length of duct w=0.5 ! half height of duct c=0.075 ! thickness of duct dpml=0.5*wavelen ! thickness of PML r=0.2 ! radius of monopole z0=c0*rho ! wave impedance in the air omega=2.*pi*freq ! angular frequency q=1./omega ! mass source x0=-r*cos(pi/4.) y0=r*sin(pi/4) et,1,220,,1 ! acoustic element et,2,220,,1,,1 ! acoustic PML element mp,dens,1,rho ! air mass density mp,sonc,1,c0 ! sound speed in the air ! generate geometry k,1,0,0,0 k,2,0,r,0 k,3,0,w,0 k,4,-d,w,0 k,5,-d,0,0 k,6,-r,0,0 k,7,x0,y0,0 k,8,-d-dpml,0 k,9,-d-dpml,w l,1,2 l,2,3 l,3,4 l,4,5 l,5,6 l,6,1 larc,2,7,1,r larc,7,6,1,r l,4,7 l,4,9 l,5,8 l,8,9 al,7,2,3,9 al,1,7,8,6 al,4,5,8,9 al,4,10,12,11 aglue,all ! generate mesh et,11,200,7 type,11 esize,h amesh,all asel,all asel,u,,,4 esize,,1 type,1 mat,1 vext,all,,,0,0,c asel,s,,,4 type,2 mat,1 esize,,1 vext,all,,,0,0,c asel,s,loc,z,0 aclear,all etdele,11 vsymm,x,all vsymm,y,all nummrg,all alls nsel,s,loc,x,-d-dpml nsel,a,loc,x,d+dpml d,all,pres,0 ! zero velocity potential on PML exterior nsel,s,loc,y,w sf,all,impd,z0,z0 ! impedance boundary on the top alls csys,1 nsel,s,loc,x,0,r bf,all,mass,q,90 ! mass source alls csys,0 nsel,all bf,all,vmen,v0,0,0, ! uniform mean flow in x-direction alls fini /solu ! solution eqslv,sparse antype,harmic harfrq,freq nsub,1 solve fini /show,png /post1 set,1,1 plns,pres ! nodal pressure fini
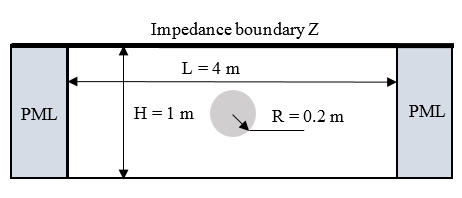
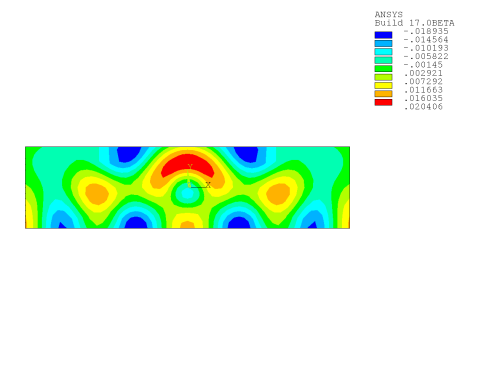
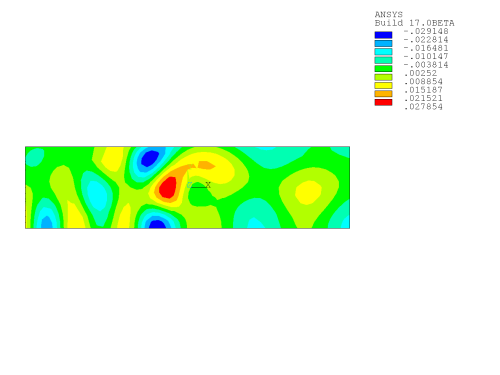
The acoustic pressures without and with mean flow are shown in the figures below.