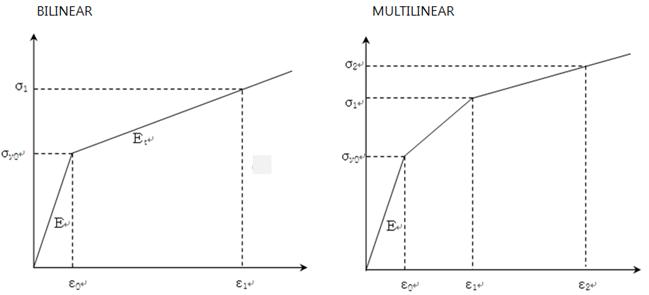
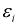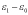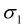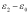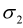A Plasticity Material has two models: BILINEAR and MULTILINEAR to represent the nominal strain-stress curve as shown in the figure below.
When using as the Linear kinematic hardening type, as the plastic deformation is increased, the corresponding yielding stress can be defined as follows:
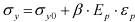 | (8–16) |
where 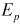 and
and 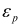 are the plastic hardening modulus and plastic
strain, respectively.
are the plastic hardening modulus and plastic
strain, respectively.
When using as the Linear kinematic hardening type, back stress is defined as follows:
(8–17) |
or equivalently,
(8–18) |
where x is back stress and c is the material constant for Prager linear hardening.
The plastic hardening modulus is calculated from the following equation.
(8–19) |
From Equation 8–79, the yielding stress and plastic strain can be calculated as the unknown variables in the Motion solver. The Cauchy stress of the plasticity material can be expressed using stretch as follows.
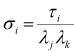 | (8–20) |
where 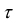 and
and 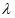 are the nominal stress and stretch,
respectively. The nominal stress can be calculated with the strain as
follows.
are the nominal stress and stretch,
respectively. The nominal stress can be calculated with the strain as
follows.
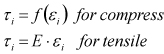 | (8–21) |
where 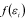 can be determined from the
strain-stress curve.
can be determined from the
strain-stress curve.
For a more detailed explanation of isotropic hardening and kinematic hardening, refer to Isotropic Hardening and Kinematic Hardening in the Material Reference.
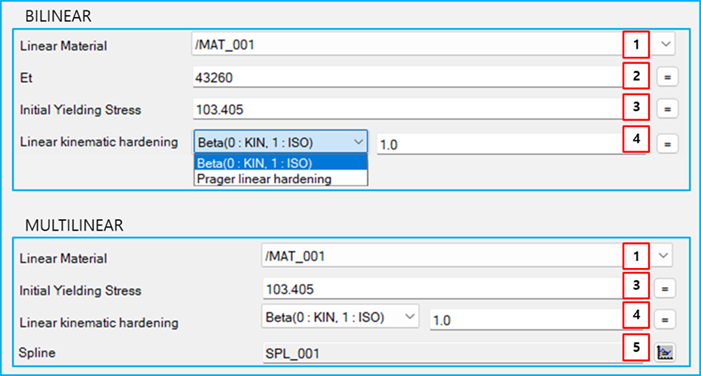
The parameters of a plasticity material are shown in the figure and table below.
Figure 8.89: Properties of a plasticity material
| Parameter | Symbol | Description | Dimension (Range) | |||||||||
| 1. Linear Material | N/A | Use to set the linear elastic material [All Models]. | N/A | |||||||||
| 2. Et |
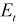 | Use to set the tangent modulus in Equation 8–19. As the value becomes zero, the material is close to the perfect plasticity. In this case, the Motion solver will more iterate to find the yielding stress [BILINEAR]. |
Force/Length^2 (Real≥0) | |||||||||
| 3. Initial Yielding Stress |
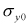 | Use to set the initial yielding stress in Equation 8–16 [All Models]. |
Force/Length^2 (Real≥0) | |||||||||
| 4. Linear kinematic hardening |
Use to set the type and value of linear kinematic hardening. The following two options are supported: and . [All Models]
where To obtain the same solution as when |
(Real≥0)
(Real≥0) | ||||||||||
| 5. Spline | N/A |
Use to set strain and stress data by Spline [MULTILINEAR]. In Spline data,
X-Data and Y-Data
are used as The difference of the strain is defined as follows.
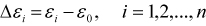
where,
|
Strain : N/A (Real≥0) Stress : Force/Length^2 (Real≥0) |
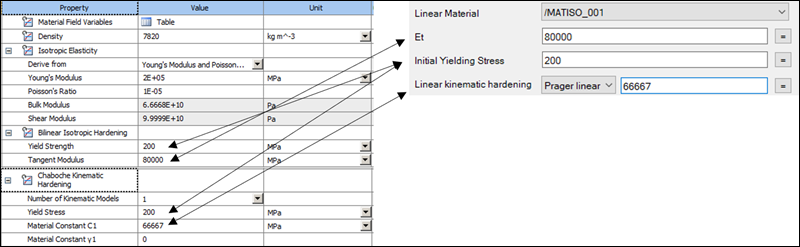
Note: In the Workbench environment, the material constant for
in Motion standalone
corresponds to the material constant C1 for
Chaboche Kinematic Hardening. The material constant
value for Chaboche Kinematic Hardening must be set to 0. To
define the tangent modulus
, add
Bilinear Isotropic Hardening to the material. In this case,
the same yield stress value must be entered for Chaboche Kinematic Hardening and
Bilinear Isotropic Hardening. If Bilinear Isotropic Hardening is not defined,
is equal to 0. See Figure 8.90: Material properties for Chaboche kinematic and Bilinear isotropic
hardening for more
details.