VM-LSDYNA-SOLVE-036
VM-LSDYNA-SOLVE-036
Adiabatic Expansion of High Explosive Detonation Products Using Eulerian
Approach
Overview
| Reference: | Lee, E.L., Hornig, H.C., & Kury, J.W. (1968). Adiabatic expansion of high explosive detonation products. Lawrence Radiation Laboratory, 1(1), 1-12. |
| Analysis Type(s): | S-ALE |
| Element Type(s): | 2D axisymmetric using Eulerian approach |
| Input Files: | Link to Input Files Download Page |
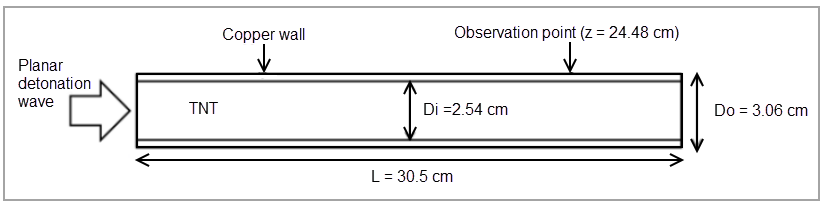
Test Case
The test case involves a copper cylinder containing TNT explosive. Detonation begins at the base of the explosive using a planar detonation wave which then travels along the axis of the cylinder. The radial expansion of the copper cylinder is measured at a specific point on its external surface (z = 24.48 cm). To measure the radial expansion, the setup uses a 2D axisymmetric model with a Eulerian formulation for the explosive and a Eulerian modeling technique for the cylinder wall.
| Geometric Properties | Material Properties |
|---|---|
|
L = 30.5 cm Do = 3.06 cm Di= 2.54 cm |
Copper: ρ = 8.96 x 10-6 g/m3 G = 45.926 GPa ν = 0.35
TNT: ρ = 1,63 x 10-6 g/m3 D = 6930 m/s PCJ = 21 GPa
Air: ρ = 1 x 10-9 g/m3 |
where
| ρ is the material density |
| G is the shear stress |
| ν is the Poisson's ratio |
| D is the detonation velocity |
| PCJ is the Chapman-Jouget pressure |
Analysis Assumptions and Modeling Notes
Since the model is axisymmetric, a 2D axisymmetric structure is used to simplify the calculations. The TNT explosive is detonated with a booster explosive which generates a planar shockwave hitting the TNT. For simplification, the detonation points are defined close enough to generate a planar detonation wave. For copper, the Gruneisen-Gamma EOS (equation of state) is used. The values can be seen in Table 7.
Table 7: Gruneisen-Gamma EOS card
| *EOS.GRUNEISEN_TITLE) (1) | |||||||
| EOSID | C | S1 | S2 | S3 | GAMMA() | A | E0 |
| 2 | 3940.0000 | 1.4890000 | 0.0 | 0.0 | 1.9700000 | 0.4700000 | 0.0 |
| V0 | UNUSED | LCID | |||||
| 1 | 0 | ||||||
For TNT, the Jones-Wilkins-Lee EOS is used. The values can be seen in Table 8.
Table 8: Jones-Wilkins-Lee EOS card
| *EOS_JWL_(TITLE) (1) | |||||||
| EOSID | A | B | R1 | R2 | OMEG | E0 | VO |
| 1 | 371.20999 | 3.7230000 | 4.1500001 | 0.9500000 | 0.3000000 | 7.0000000 | 0.0 |
For air, the Linear Polynomial EOS is used. The values can be seen in Table 9.
Table 9: Gruneisen-Gamma EOS card
| *EOS_LINEAR_POLYNOMIAL_(TITLE) (1) | |||||||
| EOSID | C0 | C1 | C2 | C3 | C4 | C5 | C6 |
| 3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.4000000 | 0.4000000 | 0.0 |
| E0 | V0 | ||||||
| 2.500E-04 | 0.0 | ||||||
Copper material must be defined like a multi-material. See Table 10.
Table 10: Multi-material card
| *ALE_STRUCTURED_MULTI-MATERIAL_GROUP_AXISYM (4) | |||||||
| AMMGNM | MID | EOSID | UNUSED | UNUSED | UNUSED | UNUSED | PREF |
| COPPER | 3 | 2 | 0.0 | ||||
The Eulerian domain is filled solely with a rigid dummy part similar to the TNT, so there is no need for Fluid-Structure Interaction (FSI). See Table 11.
Table 11: ALE_STRUCTURED_MESH_VOLUME_FILLING card
| *ALE_STRUCTURED_MESH_VOLUME_FILLING | |||||||
| MSHID | UNUSED | AMMGTO | UNUSED | NSAMPLE | UNUSED | UNUSED- | VID |
| 1 | 2 | 3 | 0 | ||||
| GEOM | IN/OUT | PID | E2 | E3 | E4 | E5 | |
| PART | 0 | 2 | 0.0 | 0 | 0 | 0 | |
Also, as the MAT Johnson-Cook (015) allows failure, a Vacuum material must be defined. See Table 12.
Table 12: Vacuum material card
| *ALE_STRUCTURED_MULTI-MATERIAL_GROUP_AXISYM (4) | |||||||
| AMMGNM | MID | EOSID | UNUSED | UNUSED | UNUSED | UNUSED | PREF |
| vacuum | 5 | 0 | 0.0 | ||||
| *MAT_VACUUM_(TITLE) (140) (1) | |||||||
| MID | RHO | ||||||
| 5 | 1.000E-09 | ||||||
Results Comparison
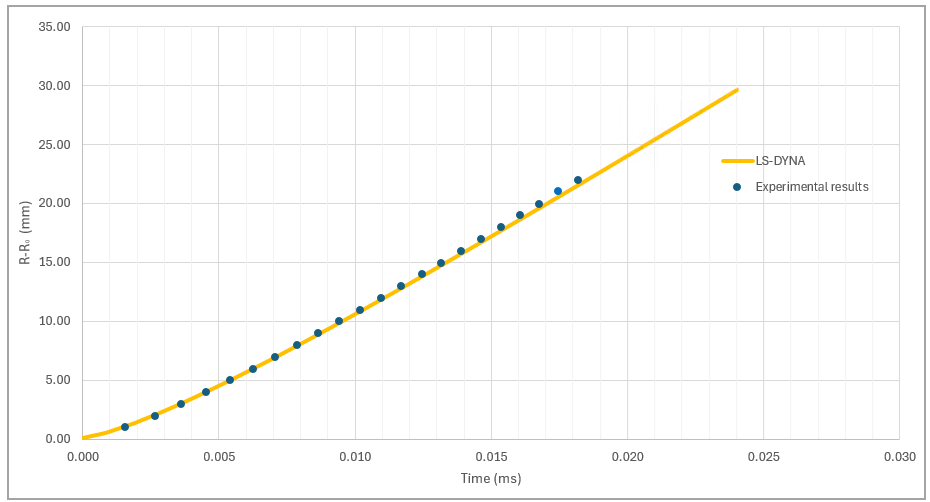
The results obtained by the LS-DYNA application are almost identical to the experimental results for R-R0—the radial expansion for the observation point at z = 24.48 cm from the moment expansion begins.
| Results | Target | LS-DYNA Solver | Error (%) |
|---|---|---|---|
| R-R0 (mm) at observation point for time 16.05 ms | 19 | 18.71 | 1.55 |