VM-WB-MECH-033

VM-WB-MECH-033
Spring Mass System Subjected to Enforced Motion with Displacement Base Excitations

Overview

Reference:

Thompson, W. T. (1999). Theory of Vibration with Applications (3rd ed., Chapter 3, pp. 63-65).

Solver(s):

Ansys Mechanical

Analysis Type(s):

Harmonic Analysis

Element Type(s):

Spring-Damper

Surface

Test Case

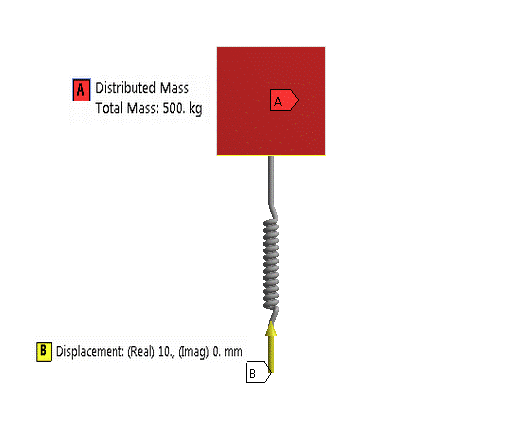
A vehicle has a mass of 500 kg (applied as distributed mass) and the total spring constant of its suspension system is 19600 N/m. The profile of the road is approximated as a sine wave of amplitude 10 mm and a wavelength of 1.5 m. Determine the amplitude of oscillations of the mass:

When driven at critical speed and having damping factor of 0.5
When driven at 50 km/h and having damping factor of 0.4

Figure 45: Schematic

Material Properties

Geometric Properties

E = 1 x 10¹³ Pa

= 1 x 10^-20 kg/m³

Mass of vehicle, m = 500 kg

Stiffness of spring, K = 19600 N/m

Sinusoidal base excitation of amplitude Y = 10 mm and wavelength

= 1.5 m

Analysis

Natural circular frequency of the system,

Critical damping coefficient,

Damping ratio,

Circular frequency of forced vibration,

Absolute amplitude of vibration,

Relative amplitude of vibration,

Absolute phase angle,

Relative phase angle,

where

m = mass of vehicle

V = speed of vehicle

Y = amplitude of sine wave

= wavelength

C = damping coefficient

Results Comparison

Results	Target	Mechanical	Error (%)
Critical speed ( = 0.99647 Hz), damping factor () of 0.5	= 14.142 mm	= 14.142 mm	0
	= -45° or 135°	= -45°	0
	= 10.00 mm	= 10.00 mm	0
	= -90° or 90°	= -90°	0
50 km/h ( = 9.26 Hz), damping factor () of 0.4	= 0.876 mm	= 0.875 mm	-0.102
	= -87.32° or -92.68°	= -92.68°	0
	= 10.079 mm	= 10.079 mm	0
	-4.98° or -175.02°	= -175.03°	0.005