5.8.2.4.1. Constraint Equation

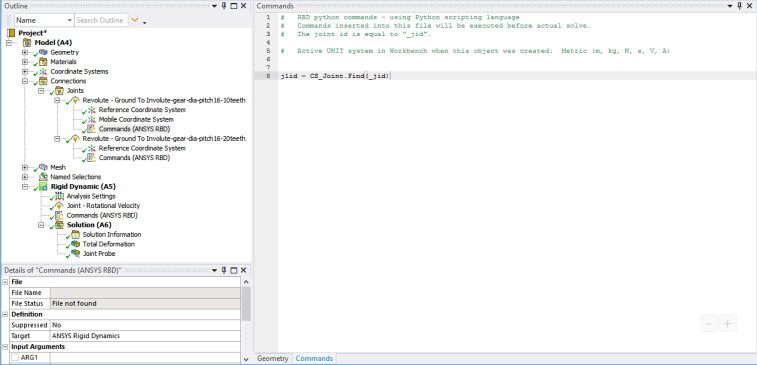
This example considers the gear mechanism shown below.

A relation is created between two revolute joints to simulate a gear with a ratio 2 M. Commands are used to enforce the ratio of velocities between the two wheels, and create a linear relation between rotational velocities, defined by:

(1)*ω ₁ + (-2)*ω₂ = 0

First, the joint objects are retrieved using their IDs:

j1id = CS_Joint.Find(_jid)
j2id = CS_Joint.Find(_jid)

Next, the relationship between the two wheels is defined. The complete list of commands is shown below. A description of these commands follows.

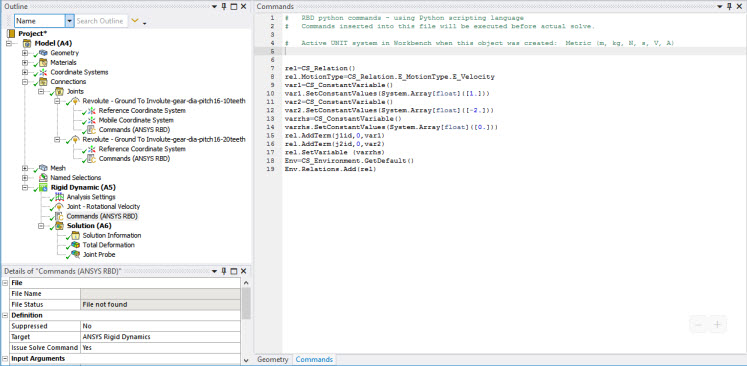
A relation object is created and specified as a relation between velocities:
```
rel=CS_Relation()
rel.MotionType=CS_Relation.E_MotionType.E_Velocity
```
The constant coefficients that appear in the relation are created. The first constant term is created by:
```
var1=CS_ConstantVariable()
var1.SetConstantValues(System.Array[float]([1.]))
```

The second coefficient and constant right hand side are created by:

var2=CS_ConstantVariable()
var2.SetConstantValues(System.Array[float]([-2.]))
varrhs=CS_ConstantVariable()
varrhs.SetConstantValues(System.Array[float]([0.]))

The first term of relation (1) X ω_1 is added to the relation object:
```
rel.AddTerm(j1id,0,var1)
```
The first argument is the joint object. The second argument defines the DOF (degrees of freedom) of the joint that are involved in the relation. Here, 0 represents the rotation, which is the joint’s first and only DOF is the rotation.
The second term and right hand side are introduced in the same manner:
```
rel.AddTerm(j2id,0,var2)
rel.SetVariable (varrhs)
```

The relation is added to the list of relations:

Env=CS_Environment.GetDefault()
Env.Relations.Add(rel)