The Jacobian ratio is a measurement of the shape of a given element compared to that of an ideal element. If an element has a bad quality Jacobian ratio, the element may not map well from element space to real space, thereby making computations based on the element shape less reliable. The ideal shape of an element depends on element type.
Jacobian ratio is not calculated for triangles and tetrahedra that are linear
(no midside nodes) or have straight-sided midside nodes. This is because the
shape function for these types of elements is linear, and the partial
derivatives of linear functions are constant. Therefore, the determinant of the
Jacobian ratio for these types of elements is constant over the entire element,
which means R J
(min) = R J
(max). For such elements, the Jacobian ratio is always
1.
Jacobian Ratio Calculation
There are two ways to calculate the Jacobian ratio: either based on corner nodes (nodal points) or based on Gauss points (integration points).
| When the Jacobian ratio calculation is based on... | Be aware that... |
| A sampling of element corner nodes |
|
| A sampling of element Gauss points |
|
An element's Jacobian ratio is computed by the following steps, using the full set of nodes for the element:
Sampling locations are based on the selected Mesh Metric option [Jacobian Ratio (MAPDL), Jacobian Ratio (Corner Nodes), or Jacobian Ratio (Gauss Points)]. At each sampling location listed in the table below, the determinant of the Jacobian matrix is computed and called RJ. RJ at a given point represents the magnitude of the mapping function between element natural coordinates and real space. In an ideally-shaped element, RJ is relatively constant over the element, and does not change sign.
Element Shape RJ Sampling Locations for Jacobian Ratio (MAPDL) and Jacobian Ratio (Corner Nodes) RJ Sampling Locations for Jacobian Ratio (Gauss Points) 10-node tetrahedra Corner nodes Four Gauss quadrature points 5-node or 13-node pyramids Base corner nodes and near apex node (apex RJ factored so that a pyramid having all edges the same length will produce a Jacobian ratio of 1) 5-node pyramids use 1 Gauss quadrature point
13-node pyramids use 8 Gauss quadrature points
8-node quadrilaterals Corner nodes and centroid Four Gauss quadrature points 20-node bricks All nodes and centroid Eight Gauss quadrature points all other elements Corner nodes Choose the optimal number of Gauss quadrature points for integration For Jacobian Ratio (MAPDL), the Jacobian ratio of the element is the ratio of the maximum to the minimum sampled value of RJ, while for Jacobian Ratio (Corner Nodes) and Jacobian Ratio (Gauss Points), it is the ratio of the minimum to the maximum. For Jacobian Ratio (MAPDL), if the maximum and minimum have opposite signs, the Jacobian ratio is arbitrarily assigned to be -100 (and the element is clearly unacceptable).
If the element is a midside-node tetrahedron, an additional RJ is computed for a fictitious straight-sided tetrahedron connected to the 4 corner nodes. For Jacobian Ratio (MAPDL), if that RJ differs in sign from any nodal RJ (an extremely rare occurrence), the Jacobian ratio is arbitrarily assigned to be -100. For Jacobian Ratio (Corner Nodes) and Jacobian Ratio (Gauss Points), the Jacobian ratio is assigned to be -1.
If the element is a line element having a midside node, the Jacobian matrix is not square (because the mapping is from one natural coordinate to 2-D or 3-D space) and has no determinant. For this case, a vector calculation is used to compute a number which behaves like a Jacobian ratio. This calculation has the effect of limiting the arc spanned by a single element to about 106°.
The Jacobian ratio of various element shapes may worsen as follows:
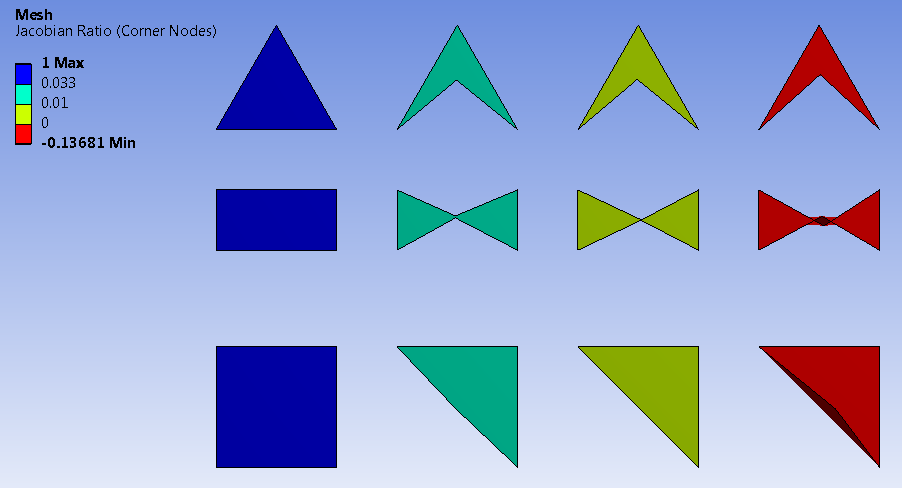
A triangle or tetrahedron has a Jacobian ratio of 1 if each midside node, if any, is positioned at the average of the corresponding corner node locations. This is true no matter how otherwise distorted the element may be. Hence, this calculation is skipped entirely for such elements. Moving a midside node away from the edge midpoint position will worsen the Jacobian ratio. If the node is moved significantly, the Jacobian ratio will become negative and the element is invalid.
Any rectangle or rectangular parallelepiped having no midside nodes, or having midside nodes at the midpoints of its edges, has a Jacobian ratio of 1. Moving midside nodes toward or away from each other can worsen the Jacobian ratio. If the node is moved significantly, the Jacobian ratio will become negative and the element is invalid.
A quadrilateral or brick has a Jacobian ratio of 1 if (a) its opposing faces are all parallel to each other, and (b) each midside node, if any, is positioned at the average of the corresponding corner node locations. As a corner node moves near the center, the Jacobian ratio worsens. If the node is moved significantly, the Jacobian ratio will become negative and the element is invalid.
The figures below illustrate mesh quality by color for Jacobian Ratio (MAPDL) and Jacobian Ratio (Corner Nodes).
Note: To view mesh quality by color, in the Details view, set Display Style to the desired metric. The use of Display Style to color mesh according to quality and the use of mesh metrics to view quality statistics are mutually exclusive. For example, when you are viewing mesh metrics, you cannot also view the mesh quality by color.
Jacobian Ratio (Gauss Points) is a good indicator of quality for quadratic tetrahedrons because its formulation is similar to that used by the solver. However, it is not very helpful for shell meshes. For shell meshes, Element Quality is a better indicator of mesh quality. For example, the 2D elements that register as bad in the preceding figures will not necessarily register as bad elements for the Jacobian Ratio (Gauss Points) mesh metric, as shown below: