Depending on the type of problem, adaptive meshing method uses two types of techniques:
Recursive subdivision of elements
A segment is divided into 2.
A 2D planar surface is divided into 4.
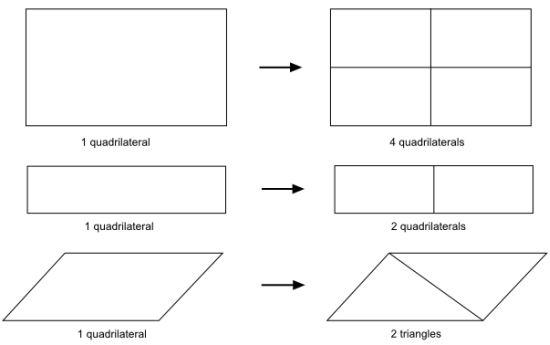
A shell quadrilateral can be subdivided into one of the following:
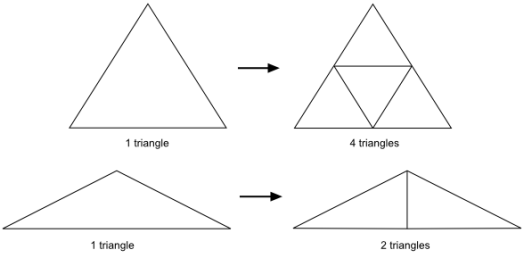
A shell triangle can be subdivided into one of the following:
A brick or wedge is divided into 8.
A tetrahedron is divided into 12.
A pyramid is divided into 10.
Note that during the subdivision, an element may be subdivided while its neighbor is not, resulting in a non-conformal mesh. In such cases, the solver creates "constraints of conformity" for the midface and/or midsegment nodes, in order to guarantee the continuity of the fields (for example, velocity, stresses, temperature, and thickness).
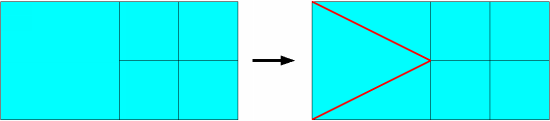
For 2D and shell meshes, you can specify that a "conformalization" step is undertaken after subdivision, during which the elements adjacent to the subdivided elements are replaced with elements that yield a conformal mesh (see Figure 16.17: Example of Conformalization). Conformalization therefore avoids the automatic creation of constraints of conformity.
Triangular / tetrahedral element generation
A triangle or tetrahedron is replaced by multiple elements of the same type (smaller and/or with a better shape).
This method is available only for triangles in 2D and tetrahedra in 3D.
For MST simulations and simulations involving species (concentration fields) transport, the recursive subdivision technique is used. For simulations with fixed meshes, the subdivision technique is used to catch large variations of fields (velocity, viscoelastic tensions, and so on).
For blow molding simulations (that is, simulations involving contact), the recursive subdivision technique is used with shell elements and tetrahedral element generation is used with volume elements. For simulations that use the Thompson, Lagrangian, elastic, or improved elastic remeshing methods, triangular / tetrahedral element generation is used for all cases except for shell blow molding (as noted above). The two methods cannot be used simultaneously.
Note: When using triangular / tetrahedral element generation for adaptive meshing, the domains that will be remeshed have to be composed with triangles in 2D or tetrahedra in 3D.