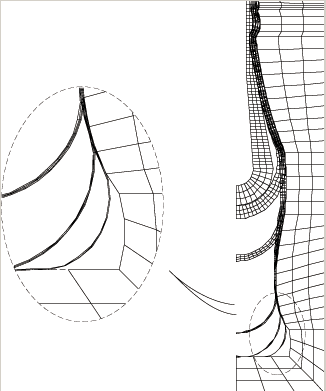
The thin shell remeshing process is characterized by large deformations in the direction tangent to the parison (in 3D, we refer to the 2D subspace tangent to the surface), combined with a relatively small thickness. In addition, the regularity of the mesh topology is such that it can be organized in a system of spines generated in the thickness of the parison. Figure 16.8: 2D Axisymmetric Blow Molding Problem shows a 2D axisymmetric blow molding problem on which the thin shell remeshing method is to be used.
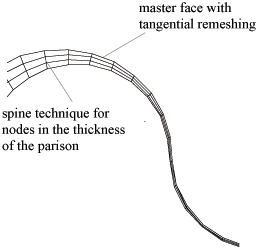
Thin shell remeshing combines tangential remeshing along a single free surface (or interface) called the master free surface with a spine rule in the thickness of the parison. In other words, a tangential remeshing is applied to one of the free surfaces, in order to keep an acceptable element distribution within the mesh. The internal nodes are relocated along spines that are defined as geometrically normal to the master free surface.
The procedure is as follows:
You select the master free surface among all free surfaces and moving interfaces. It is common to select the boundary set that will come into contact with the mold.
The system of spines is automatically built as the set of nodes connected through mesh segments to each node of the master free surface.
In multilayer applications, you must select a remeshing rule of the thin shell type in each sub-task (one for each layer). However, definition of the master free surface is unique throughout all remeshing rules of the thin shell type currently defined. See User Inputs for Remeshing for information about inputs for this remeshing method.
Nodes of the master free surface are tangentially remeshed using a 1D proportionality rule (for 2D problems) or a 2D Optimesh rule (for 3D problems). The internal nodes are proportionally relocated with the spine technique; for each spine, the internal nodes are relocated along a direction geometrically normal to the master surface. Figure 16.9: The Effect of Tangential Remeshing in the Case of Large Deformations illustrates the application of the thin shell remeshing rule.
In 2D, the thin shell remeshing technique preserves the node distribution originally introduced along the master free surface. Note that the standard Thompson remeshing technique is not recommended when the parison is thin, because element distortion in the normal direction might then become large.
In 3D, nodes will be relocated tangentially on the master free surface at the beginning of the calculation. Nodes located on the boundary of the master surface (that is, along 1D curves) will follow material lines, in order to provide the Optimesh rule with appropriate boundary conditions. Due to the constraint that prevents boundary nodes from moving for very small time steps, displacements of the original mesh on the master surface are rather limited, and the convergence behavior is generally good.