VM-LSDYNA-SOLVE-020
VM-LSDYNA-SOLVE-020
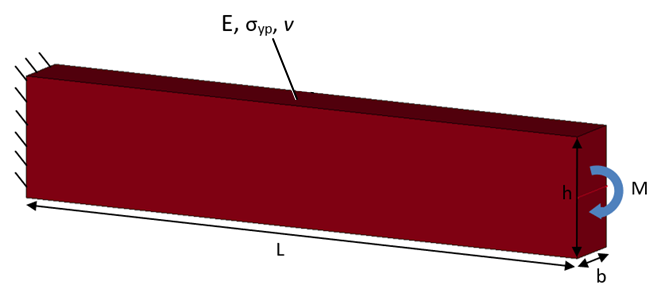
Elasto-Plastic Analysis of a Rectangular Beam
Overview
| Reference: | Any solid mechanics textbook |
| Analysis Type(s): | Static Plastic Analysis |
| Element Type(s): | Shell |
| Input Files: | Link to Input Files Download Page |
Test Case
This test case also appears in the Workbench Mechanical Verification Manual. See VM-WB-MECH-029.
A rectangular beam is loaded in pure bending. For an elastic-perfectly-plastic stress-strain behavior, show that the beam remains elastic at M = Myp = σypbh2/6 and becomes completely plastic at M = Mult = 1.5 Myp.
| Material Properties | Geometric Properties | Loading |
|---|---|---|
| E = 30,000,000 psi | Length, L = 10 in | M = 1.0 Myp = 24,000 lbf-in |
| σyp = 36,000 psi | Width, b = 1 in | M = 1.25 Myp = 30,000 lbf-in |
| v = 0.0 | Height, h = 2 in | M = 1.5 Myp = 36,000 lbf-in |
Analysis Assumptions and Modeling Notes
The rectangular beam is made of ten shell elements using ELFORM 2 and thickness 2 inches. The number of through thickness integration points is set to eight with NIP in *SECTION_SHELL. Lobatto integration is specified in *CONTROL_SHELL to measure integration point stress on the shell surfaces. Material properties including yield strength are defined in *MAT_PLASTIC_KINEMATIC. ETAN is set to zero to make an elastic-perfectly-plastic model.
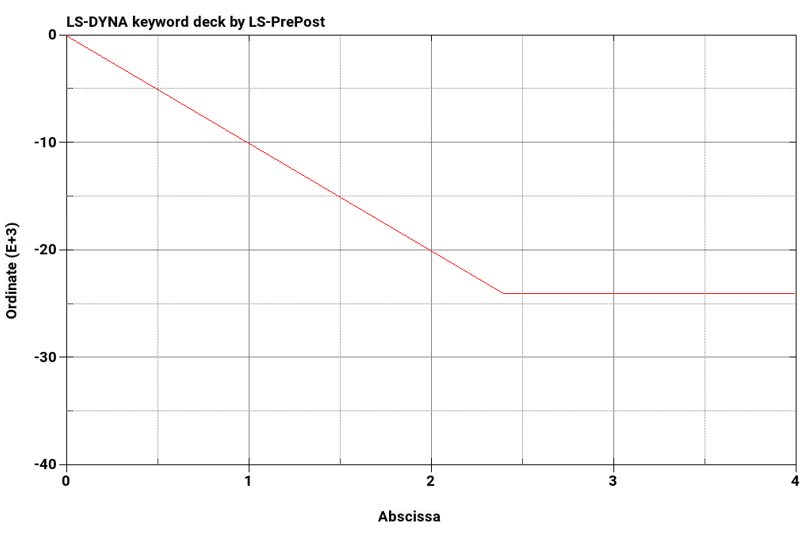
*BOUNDARY_SPC_SET creates a fixed support at one end of the beam. The opposite end face was made rigid using a *CONSTRAINED_NODAL_RIGID_BODY. This was necessary to apply a moment to the tip of the beam. The moment was prescribed using *LOAD_RIGID_BODY. Implicit analysis is used with NSOLVER 12. Static analysis is specified with IMASS in *CONTROL_IMPLICIT_DYNAMICS.
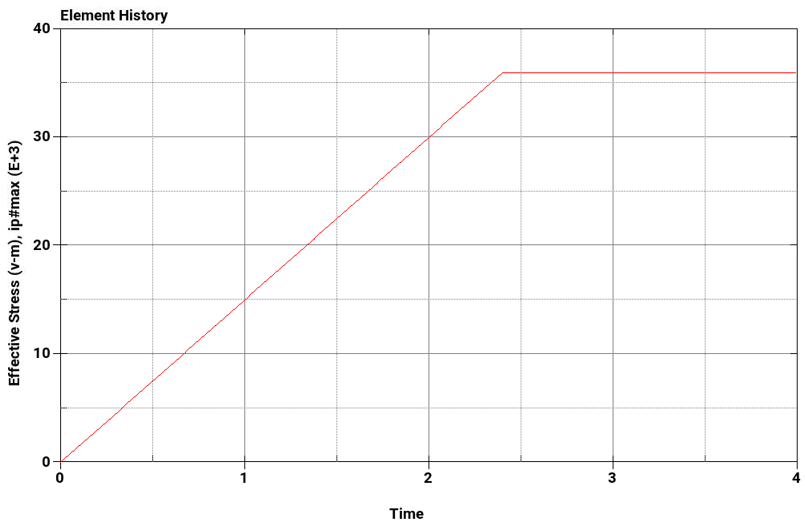
The maximum von mises stress is measured from d3plot using the History tool in LS-PrePost.
Results Comparison
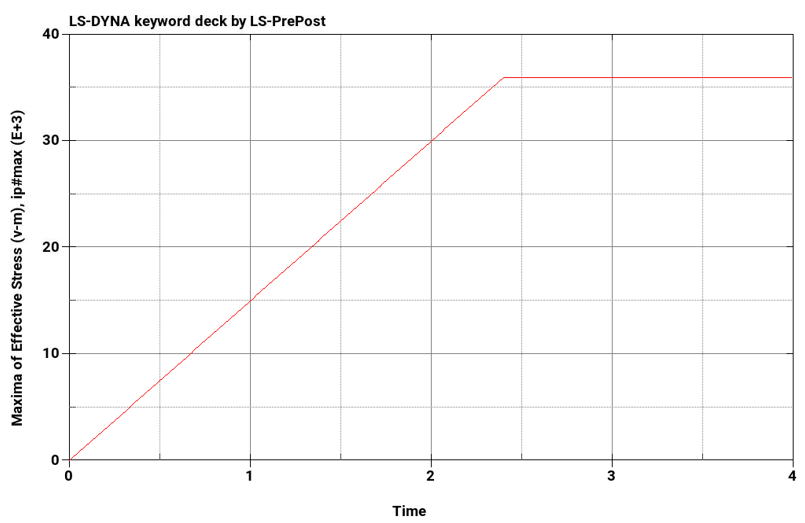
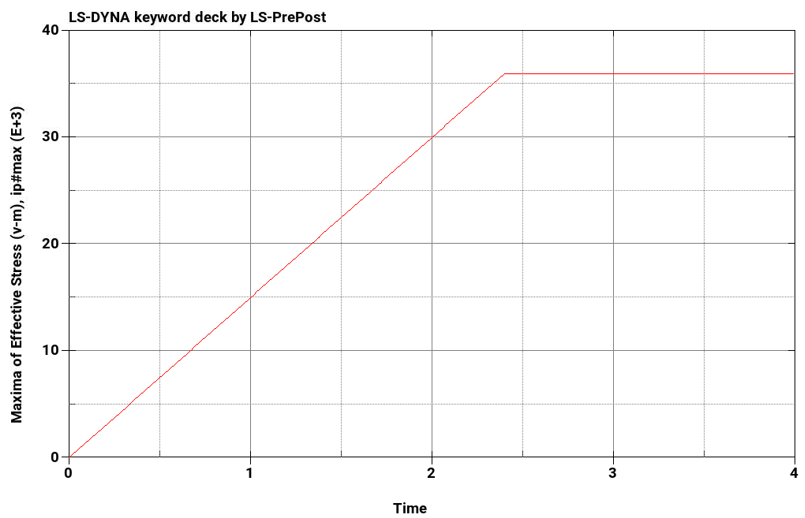
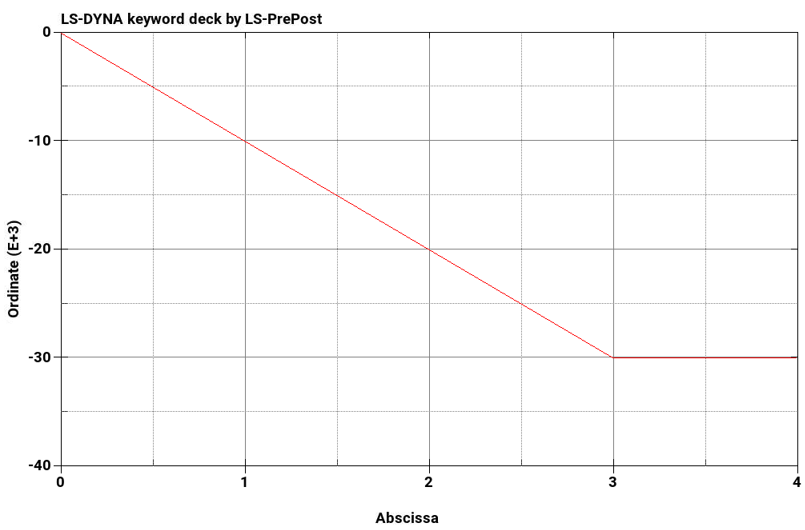
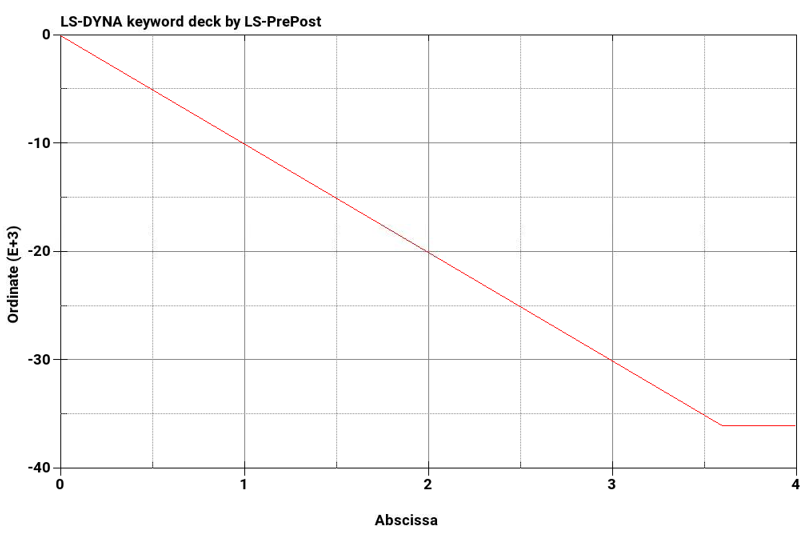
Below are three sets of column plots. The first plot shows the maximum von mises stress with respect to time for M = 24000, 30000, and 36000 lbf-in, respectively. The second plot shows the applied moment with respect to time. The rate of applied moment is equal in each test case. Results show that the beam becomes plastic once a stress of 36000 psi is reached.
| Results | Target | LS-DYNA | Error (%) |
|---|---|---|---|
|
Equivalent Stress, psi for M = 24000 lbf-in | 36000 | 36000 | 0.0 |
|
Equivalent Stress, psi for M = 30000 lbf-in | 36000 | 36000 | 0.0 |
|
Equivalent Stress, psi for M = 36000 lbf-in | 36000 | 36000 | 0.0 |