VM-WB-MECH-029

VM-WB-MECH-029
Elasto-Plastic Analysis of a Rectangular Beam

Overview

Reference:	Timoshenko, S. (1956). Strength of Material, Part II: Elementary Theory and Problems (3rd Edition). New York, NY: D. Van Nostrand Co. (Article 64) 349.
Solver(s):	Ansys Mechanical
Analysis Type(s):	Static Plastic Analysis
Element Type(s):	Solid

Test Case

A rectangular beam is loaded in pure bending. For an elastic-perfectly-plastic stress-strain behavior, show that the beam remains elastic at M = M_yp = σ_ypbh² / 6 and becomes completely plastic at M = M_ult = 1.5 M_yp.

Figure 32: Problem Sketch

Figure 33: Stress-Strain Curve

Figure 34: Workbench Model

Bilinear Kinematic Hardening Material Properties

Geometric Properties

Loading

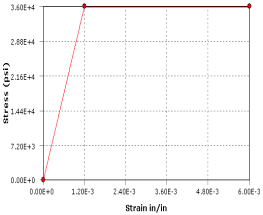
Young's Modulus E = 30 x 10⁶ psi

Yield Strength σ_yp = 36000 psi

Tangent Modulus = 0 psi

Poisson's Ratio ν = 0.0

Length L = 10 in

Width B = 1 in

Height H = 2 in

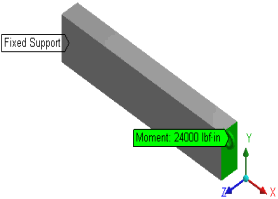
M = 1.0 M_yp to 1.5 M_yp

(M_yp = 24000 lbf - in)

Applied in four steps

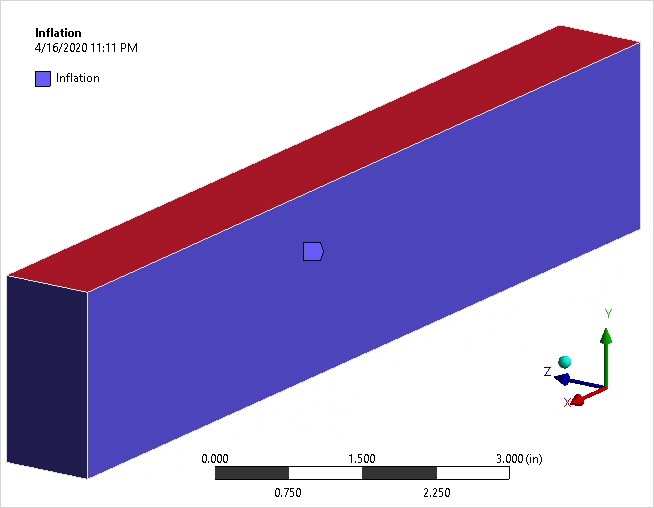
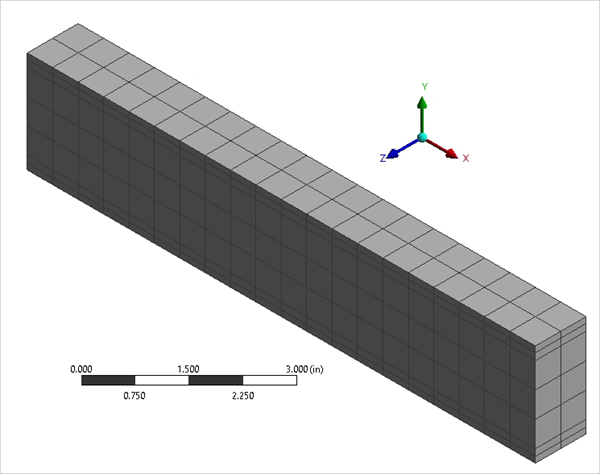
Mesh Controls and Symmetry

Inflation mesh control is added to the body using the top and bottom faces as the boundaries. The MultiZone Mesh Method is set to Hexa as Mapped Mesh Type and Quadratic (Higher Order) Element Order. A symmetric boundary condition is applied in the global Z direction on the vertical face of the beam.

Figure 35: Inflation Image

Figure 36: Symmetry Image

Figure 37: Mesh Image

Analysis

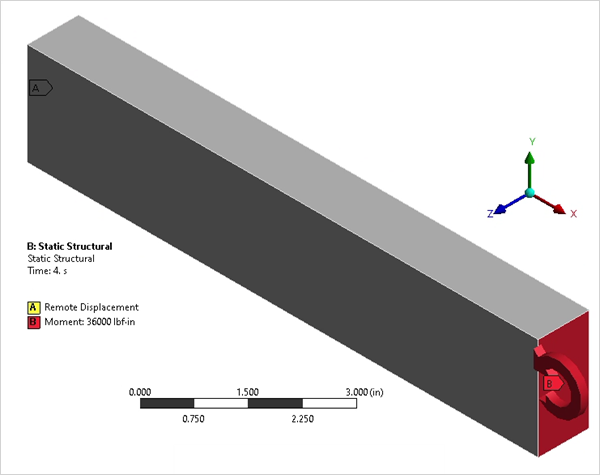
Manual Mesh Control is set to Geometry, and Full Brick Integration Scheme is selected for the analysis. Two Remote Points are created, one on each end face with Rigid behavior for applying the load and for setting the boundary conditions. One end of the beam is fixed by applying Remote Displacement scoped to Remote Point. Moment load is applied on the other end using Remote Point in four steps: M1 = 24000 lbf-in, M2 = 28000 lbf-in, M3 = 32000 lbf-in and M4 = 36000 lbf-in. Analysis settings for Force and Displacement Convergence are set to On.

Figure 38: Loading and Boundary Condition

Results Comparison

Moment load is applied in four steps, and Directional Deformation in the Y direction on the center node of the free face (on which Moment load is applied) is compared.

Because solid elements do not calculate node rotation at the free end, directional deformation is used as the target for validating results.

M/M_yp	Target		Mechanical		Error (%)
	State	Directional Deformation (in)	State	Directional Deformation (in)
1	fully elastic	0.06	fully elastic	0.060001	0.002
1.1666	elastic-plastic	0.072964	elastic-plastic	0.072846	-0.162
1.3333	elastic-plastic	0.10136	elastic-plastic	0.10103	-0.3256
1.5	plastic	solution not converged	plastic	solution not converged	-