In the LES approach, the filtered flow quantities are solved by the transport equations on
the CFD mesh. For example,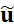 
now refers to the filtered flow velocity. The undetermined stress term 
in Equation 2–3
is called the sub-grid-scale
(SGS) stress tensor, which is essential in LES modeling. Ansys Forte offers two types of LES
models, the Smagorinsky model and the dynamic structure model.
The Smagorinsky model [89] is based on a viscosity assumption and accounts for the dissipative nature of turbulent flows, that is, kinetic energy is dissipated from the large-scale to the small-scale motions. It relates the SGS stress to the strain rate of the filtered flow field:
 | (2–30) |
The SGS viscosity, 
, is modeled as:
 | (2–31) |
in which 
is the local CFD mesh size, 
is the magnitude of the filtered strain rate tensor (see Equation 2–25
, but note that the overbar 
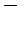now means filtering), and 
is a model constant, 0.17. The sub-grid kinetic energy, 
, is modeled as:
 | (2–32) |
where 
is a model constant, 0.101. It is noted that both 
and 
depend on the CFD mesh size, .
The sub-grid flux term 
in the species transport Equation 2–1
is modeled as:
 | (2–33) |
in which 
is the SGS turbulent diffusivity. Similarly, the sub-grid flux term H in the energy equation (Equation 2–5
) is modeled as:
 | (2–34) |
in which 
is the SGS thermal conductivity and is related to the SGS thermal diffusivity 
and heat capacity 
by 
. The SGS mass and thermal diffusivity are related to the SGS viscosity
by:
 | (2–35) |
 | (2–36) |
where 
and 
are the turbulent Schmidt and Prandtl numbers, respectively. The
viscosity-based assumption makes Smagorinsky model effective in dissipating the kinetic energy
from large-scale to small-scale motions. However, such dissipation can be excessive, and
energy-containing flow structures may not be adequately resolved unless a very fine mesh is
used. Although, its numerical stability in complex flows is an advantage.
The dynamic structure model [71] is a non-viscosity and similarity-based model, relating the SGS stress to the “Leonard stress” derived from a larger filter:
 | (2–37) |
where L is the Leonard stress tensor, 
, and 
. An explicit filtering operation (denoted as 
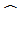) needs to be performed to compute the Leonard stress tensor, and the
explicit filter size is chosen as twice of the local CFD mesh size. Essentially, the first term
on the right-hand-side of Equation 2–37
can
be viewed as a similarity model relating the SGS stress to the Leonard stress, with a dynamic
scaling factor of 
representing the ratio of sub-grid kinetic energy to sub-filter kinetic
energy. The second term is an optional added viscosity-based model [96]
. It is suggested to be activated for fuel
injection and spray simulations for numerical stability purposes. The viscosity is modeled
as
 | (2–38) |
where 
and 
. The symbols 
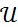and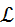 
are injection velocity and nozzle diameter in sprays.
To use the dynamic structure model, the sub-grid flux terms 
and 
can still adopt the viscosity-based models shown in Equation 2–33 and Equation 2–34
. The SGS
viscosity is calculated as:
 | (2–39) |
where 
. A transport equation for the sub-grid kinetic energy, 
, needs to be solved to provide closure
 | (2–40) |
where 
. The dissipation rate of the sub-grid kinetic energy has been modeled as
.
The dynamic structure model offers good prediction of the sub-grid stresses [81] , and has been validated in a number of benchmark flow problems [96] , [98] . Note that in view of our best practice recommendations in engine flow simulations, the Smagorinsky model is recommended as the default option due to its superior numerical stability in dealing with flows near compelx boundaries.