Newman’s group developed a physics based model using porous electrode and concentrated solution theories [[148]]. The model can accurately capture Li-ion migration in the battery. It has been widely used in the literature [[612], [90]].

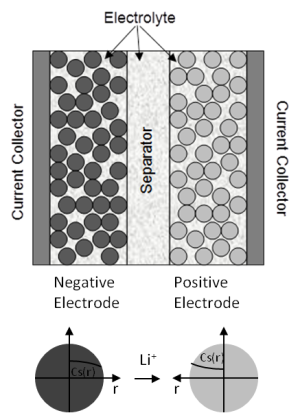
Figure 19.2: Electrode and Particle Domains in the Newman’s Model schematically shows the electrode plate pair in the Li-ion battery. The composite electrode consists of active materials and electrolyte solution. The electrolyte phase is continuous across the negative electrode, separator and positive electrode while solid phase only exists in the negative and positive electrode. The solid active material is modeled as a matrix of mono-sized spherical particles.

Figure 19.2: Electrode and Particle Domains in the Newman’s Model

During the discharge process, Li diffuses to the surface of negative electrode particles and undergoes an electrochemical reaction. This reaction releases an electron and transfers Li to the electrolyte phase. The Li-ions diffuse and conduct through the electrolyte solution from the negative electrode to the positive electrode, where a similar reaction transfers Li to the positive solid phase. Li is stored inside the positive electrode particles until the cell is later recharged.

The Li-ion transport phenomena in the porous electrode and electrolyte can be described by the charge and mass conservation laws. Charge conservation governs phase potentials, and , while mass conservation governs the phase concentrations, and , where the subscripts and are used to denote the electrolyte and solid (electrode) phases, respectively.

The conservation equations relevant to electrolyte and solid phases are described as:

The Lithium conservation diffusion equation must be solved at every discretized spatial location in the electrode zone. The Lithium conservation equation is solved in the r-dimension of the spherical particles—the pseudo second dimension. That is why the model is often referred to as the Newman’s P2D model in the literature.

The Butler-Volmer equation is used to couple the charge and species governing equations by describing the current flux at the active material pore-wall surface due to lithium intercalation reaction as a function of overpotential, :

(19–18)

where is defined by

(19–19)

and is the exchange current density defined by

(19–20)

The last term on the right-hand side of Equation 19–19 is the potential drop due to the electric resistance of the electrode particle surface film.

Effective properties are used in the above equations in which the electrolyte ionic diffusivity, conductivity, diffusional conductivity, and solid phase electric conductivity are defined as:

(19–21)

(19–22)

(19–23)

(19–24)

(19–25)

(19–26)

(19–27)

Note that the sum of the volume fractions of electrolyte and active and filler materials must sum to unity:

(19–28)

The above equations use the following notations:

The source terms for the potential equations (Equation 19–4) and the energy equation (Equation 19–3) is computed as:

(19–29)

(19–30)

where , , and are the thicknesses of positive electrode, negative electrode, and separator, respectively, and is the transverse current density

(19–31)

In practice, the Newman's P2D model is solved on the electrode scale. is usually based on the unit area of electrode. Equation 19–29 is used to connect the current transfer rate at the battery cell scale to the electrode scale.

For more information about setting up the Newman’s P2D Model, see Inputs for the Newman’s P2D Model.