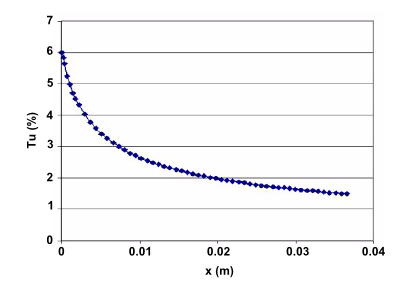
It has been observed that the turbulence intensity specified at an inlet can decay quite rapidly depending on the inlet viscosity ratio () (and hence turbulence eddy frequency). As a result, the local turbulence intensity downstream of the inlet can be much smaller than the inlet value (see Figure 4.5: Exemplary Decay of Turbulence Intensity (Tu) as a Function of Streamwise Distance (x)). Typically, the larger the inlet viscosity ratio, the smaller the turbulent decay rate. However, if too large a viscosity ratio is specified (that is, > 100), the skin friction can deviate significantly from the laminar value. There is experimental evidence that suggests that this effect occurs physically; however, at this point it is not clear how accurately the transition model reproduces this behavior. For this reason, if possible, it is desirable to have a relatively low (that is, 1 – 10) inlet viscosity ratio and to estimate the inlet value of turbulence intensity such that at the leading edge of the blade/airfoil, the turbulence intensity has decayed to the desired value. The decay of turbulent kinetic energy can be calculated with the following analytical solution:

(4–191)

For the SST turbulence model in the freestream the constants are:

(4–192)

The time scale can be determined as follows:

(4–193)

where is the streamwise distance downstream of the inlet and is the mean convective velocity. The eddy viscosity is defined as:

(4–194)

The decay of turbulent kinetic energy equation can be rewritten in terms of inlet turbulence intensity () and inlet eddy viscosity ratio () as follows:

(4–195)

Figure 4.5: Exemplary Decay of Turbulence Intensity (Tu) as a Function of Streamwise Distance (x)

You should ensure that the values around the body of interest roughly satisfy >0.1%. For smaller values of , the reaction of the SST model production terms to the transition onset becomes too slow, and transition can be delayed past the physically correct location.