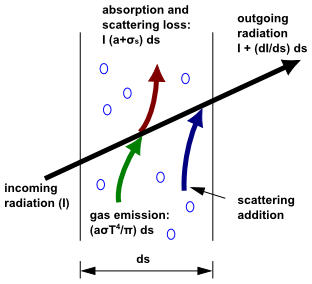
The radiative transfer equation (RTE) for an absorbing, emitting,
and scattering medium at position in the direction
is
(5–22) |
|
where | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
|
is the
optical thickness or opacity of the medium. The refractive index
is important when considering
radiation in semi-transparent media. Figure 5.1: Radiative Heat Transfer illustrates the process of radiative heat transfer.
The DTRM, P-1, Rosseland, DO, and MC radiation models require the absorption coefficient
as input.
and the scattering coefficient
can be constants, and
can also be a function of local concentrations of
and
, path length, and total pressure. Ansys Fluent provides
the weighted-sum-of-gray-gases model (WSGGM) for computation of a variable absorption
coefficient. For details, see Radiation in Combusting Flows. The DO and MC
implementations can model radiation in semi-transparent media. The refractive index
of the medium must be provided as a part of the calculation for this type of
problem. The Rosseland model also requires you to enter a refractive index, or use the default
value of
.
The P-1 and DO radiation model is solved for the mixture material. Radiative properties, such as the absorption coefficient, refractive index, and scattering coefficients of the mixture, are computed based on the volume fraction based averaging of the radiative properties of the individual phases.
In simulations that use the porous media model with a radiation model, the contributions of the radiative heat flux and radiative heat source in the energy calculation are scaled by the local porosity. Note that the modeling treatment for the interaction of porous media and radiation in Ansys Fluent is strictly valid only for values of local fluid porosity that are very close or equal to 1.0.