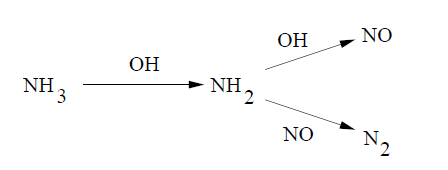
Several investigators have modeled the process using a large number of elementary reactions. A simple empirical model has been proposed by Fenimore [172], which is based on experimental measurements. However, the model was found to be unsuitable for practical applications. Ostberg and Dam-Johansen [501] proposed a two-step scheme describing the SNCR process as shown in Figure 9.2: Simplified Reaction Mechanism for the SNCR Process, which is a single initiation step followed by two parallel reaction pathways: one leading to NO reduction, and the other to NO formation.

Figure 9.2: Simplified Reaction Mechanism for the SNCR Process

(9–88)

(9–89)

The reaction orders of NO and NH₃ at 4% volume O₂ and the empirical rate constants and for Equation 9–88 Equation 9–89, respectively, have been estimated from work done by Brouwer et al. [82]. The reaction order of NO was found to be 1 for Equation 9–88 and the order of NH₃ was also found to be 1 for both reactions. As such, the following reaction rates for NO and NH₃, at 4% volume O₂, were proposed:

(9–90)

(9–91)

The rate constants and have units of m³/mol-s, and are defined as

where J/mol and J/mol.

This model has been shown to give reasonable predictions of the SNCR process in pulverized coal and fluidized bed combustion applications. The model also captures the influence of the most significant parameters for SNCR, which are the temperature of the flue gas at the injection position, the residence time in the relevant temperature interval, the NH₃ to NO molar ratio, and the effect of combustible additives. This model overestimates the NO reduction for temperatures above the optimum temperature by an amount similar to that of the detailed kinetic model of Miller and Bowman [439].

Urea as a reagent for the SNCR process is similar to that of injecting ammonia, and has been used in power station combustors to reduce NO emissions successfully. However, both reagents, ammonia and urea, have major limitations as a NO_x reducing agent. The narrow temperature “window” of effectiveness and mixing limitations are difficult factors to handle in a large combustor. The use of urea instead of ammonia as the reducing agent is attractive because of the ease of storage and handling of the reagent.

The SNCR process using urea is a combination of Thermal DeNOx (SNCR with ammonia) and RAPRENOx (SNCR using cyanuric acid that, under heating, sublimes and decomposes into isocyanic acid), because urea most probably decomposes into ammonia and isocyanic acid [439].

One problem of SNCR processes using urea is that slow decay of HNCO, as well as the reaction channels leading to N₂O and CO, can significantly increase the emission of pollutants other than NO. Urea seems to involve a significant emission of carbon-containing pollutants, such as CO and HNCO.

Also, some experimental observations [560] show that SNCR using urea is effective in a narrow temperature window that is shifted toward higher temperatures, when compared to Thermal DeNOx processes at the same value of the ratio of nitrogen in the reducing agent and the NO in the feed, , where is defined as the ratio of nitrogen in the reducing agent and NO in the feed. The effect of increasing the value is to increase the efficiency of abatement, while the effect of increasing O₂ concentration depends on the temperature.

The model described here is proposed by Brouwer et al. [82] and is a seven-step reduced kinetic mechanism. Brouwer et al. [82] assumes that the breakdown of urea is instantaneous and 1 mole of urea is assumed to produce 1.1 moles of NH₃ and 0.9 moles of HNCO. The work of Rota et al. [560] proposed a finite rate two-step mechanism for the breakdown of urea into ammonia and HNCO.

The seven-step reduced mechanism is given in Table 9.2: Seven-Step Reduced Mechanism for SNCR with Urea, and the two-step urea breakdown mechanism is given in Table 9.3: Two-Step Urea Breakdown Process.

Table 9.2: Seven-Step Reduced Mechanism for SNCR with Urea

Reaction	A	b	E
	4.24E+02	5.30	349937.06
	3.500E-01	7.65	524487.005
	2.400E+08	0.85	284637.8
	1.000E+07	0.00	-1632.4815
	1.000E+07	0.00	0
	2.000E+06	0.00	41858.5
	6.900E+17	-2.5	271075.646

Table 9.3: Two-Step Urea Breakdown Process

Reaction	A	b	E
	1.27E+04	0	65048.109
	6.13E+04	0	87819.133

where SI units (m, mol, sec, J) are used in Table 9.2: Seven-Step Reduced Mechanism for SNCR with Urea and Table 9.3: Two-Step Urea Breakdown Process.

When the SNCR model with urea injection is employed in addition to the usual transport equations, Ansys Fluent solves the following three additional mass transport equations for the urea, HNCO, and NCO species.

(9–92)

(9–93)

(9–94)

where , and are mass fractions of urea, HNCO, and NCO in the gas phase. The source terms , , and are determined according to the rate equations given in Table 9.2: Seven-Step Reduced Mechanism for SNCR with Urea and Table 9.3: Two-Step Urea Breakdown Process and the additional source terms due to reagent injection. These additional source terms are determined next. The source terms in the transport equations can be written as follows:

(9–95)

(9–96)

(9–97)

Apart from the source terms for the above three species, additional source terms for NO, NH₃, and N₂O are also determined as follows, which should be added to the previously calculated sources due to fuel NO_x:

(9–98)

(9–99)

(9–100)

The source terms for species are determined from the rate equations given in Table 9.2: Seven-Step Reduced Mechanism for SNCR with Urea and Table 9.3: Two-Step Urea Breakdown Process.

The rate of urea production is equivalent to the rate of reagent release into the gas phase through droplet evaporation:

(9–101)

where is the rate of reagent release from the liquid droplets to the gas phase (kg/s) and is the cell volume (m³).

If the urea decomposition model is set to the user-specified option, then the rate of NH₃ production is proportional to the rate of reagent release into the gas phase through droplet evaporation:

(9–102)

where is the rate of reagent release from the liquid droplets to the gas phase (kg/s), is the mole fraction of NH₃ in the NH₃/ HNCO mixture created from urea decomposition, and is the cell volume (m³).

If the urea decomposition model is set to the user-specified option, then the rate of HNCO production is proportional to the rate of reagent release into the gas phase through droplet evaporation:

(9–103)

where , the injection source term, is the rate of reagent release from the liquid droplets to the gas phase (kg/s), is the mole fraction of HNCO in the NH₃/ HNCO mixture created from urea decomposition, and is the cell volume (m³).

However, the default option for urea decomposition is through rate limiting reactions given in Table 9.3: Two-Step Urea Breakdown Process, and the source terms are calculated accordingly. In this case, both values of and are zero.