Ansys Fluent provides an alternative model for droplet breakup called KHRT ([54], [509]), which combines the effects of Kelvin-Helmholtz waves driven by aerodynamic forces with Rayleigh-Taylor instabilities due to acceleration of shed drops ejected into freestream conditions. Both mechanisms model droplet breakup by tracking wave growth on the surface of the droplet, with breakup occurring due to the fastest growing instability based on local conditions. To model the liquid core in the near nozzle region, a Levich core length is applied that only allows breakup due to Kelvin-Helmholtz wave growth.
The KHRT model was developed to simulate high Weber number sprays and should not be applied to low pressure sprays.
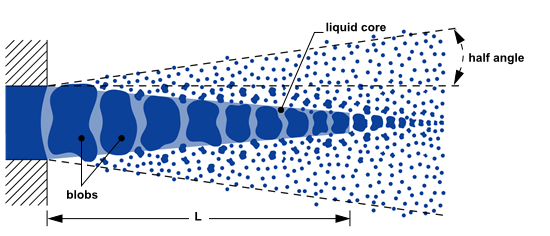
The KHRT model assumes that a liquid core exists in the near nozzle region. Child droplets are shed from this liquid core and are subjected to sudden acceleration when they are ejected into the freestream and a Rayleigh-Taylor instability becomes the dominant effect. The length of the liquid core is obtained from Levich theory [359]:
(12–438) |
Where is the Levich constant and
is a reference nozzle diameter. The reference
diameter must be specified for atomizer injections in Ansys Fluent, however
the cone and solid cone injections assume that the reference diameter
is the minimum of the droplet diameter and the inner diameter of the
cone. Surface injections use the surface area specified to calculate
an equivalent hydraulic diameter for use as
. When a Rosin-Rammler distribution is specified
for non-atomizer injections, the maximum diameter of the Rosin-Rammler
becomes the reference diameter.
A liquid core is approximated by ‘blobs’ [54] as shown in Figure 12.23: Liquid Core Approximation.
The ‘blobs’ are introduced into the domain with the diameter specified in the injection. It is often best to use an effective droplet diameter by considering a contraction coefficient, which can be computed with
(12–439) |
Where denotes the contraction coefficient.
You can disable the Liquid Core Approximation entirely by setting
the Levich constant, , to zero as described in Breakup in the Fluent User's Guide.
As with the Kelvin-Helmholtz model, the Rayleigh-Taylor (RT) model is based on wave instabilities on the droplet surface. The frequency of the fastest growing wave is computed by
(12–440) |
Where is the droplet acceleration in the direction of
the droplet travel. The corresponding wave number is given by
(12–441) |
Breakup occurs after RT waves have been growing for a time larger
than the breakup time , defined as
(12–442) |
Here is the Rayleigh-Taylor
breakup time constant which has a default value of
.
The wave growth is tracked when the predicted wave length , corresponding to the fastest
wave growth rate, is smaller than the local droplet diameter. The
radius of the smaller child droplets is calculated with
(12–443) |
where is the breakup radius constant which has a default
value of
.
Within the liquid core only aerodynamic breakup is considered. It is computed based on the Wave breakup model, described in the previous section.
Outside the liquid core, both KH and RT effects are calculated and both are considered for breakup. Typically, the RT instability grows faster when droplet acceleration is high and this effect dominates for high Weber number sprays. In both cases, a new parcel is generated only when the accumulated shed parcel mass exceeds 5% of the initial parcel mass.