In the discrete method, the particle population is discretized into a finite number of size intervals. This approach has the advantage of computing the particle size distribution (PSD) directly. This approach is also particularly useful when the range of particle sizes is known a priori and does not span more than two or three orders of magnitude. In this case, the population can be discretized with a relatively small number of size intervals and the size distribution that is coupled with fluid dynamics can be computed. The disadvantage of the discrete method is that it is computationally expensive if a large number of intervals is needed.

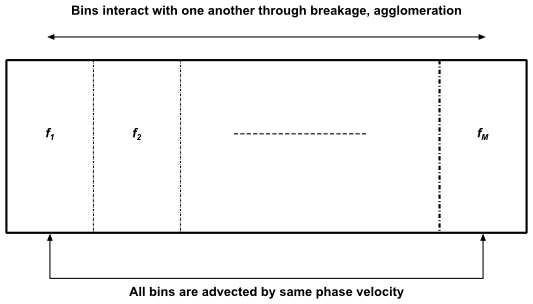
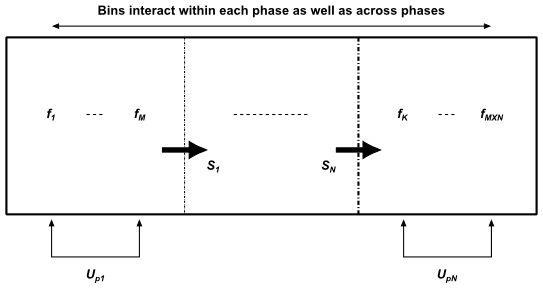
One of the limitations of the existing homogeneous discrete method is that all bins are assigned to the same secondary phase and are therefore advected with the same phase momentum. This is unsuitable for modeling cases where large and small bin sizes are likely to segregate due to different momentum fields. The inhomogeneous discrete method overcomes this limitation by allowing groups of bins to be advected by different phase velocities. Therefore when the inhomogeneous discrete model is activated, the Population Balance model can be applied to more than one secondary phase.

The general transport equation for the discrete bin fraction can be written as

(14–689)

Since all bins belong to a single phase in the homogeneous discrete method, the net mass source for the phase in case of breakage and agglomeration is zero and can be expressed as

(14–690)

This is shown schematically in Figure 14.16: Homogeneous Discrete Method where all bins are advected by the same phase velocity . In contrast, the inhomogeneous discrete method shown in Figure 14.17: Inhomogeneous Discrete Method allows bins to be assigned to multiple phases. Here bins per phase are distributed over phases for a total of bins. Bins and are advected by phase velocity and so forth. The sum of bin sources in any given phase is not necessarily equal to zero since bins in a given phase can migrate to another phase through breakage or agglomeration, thereby creating a net mass source for that phase.

The net mass source for a given phase can be expressed as the sum of the bin sources belonging to that phase

(14–691)

For breakage and coalescence the sum over all phase sources is zero

(14–692)

also similar to the homogeneous discrete model

(14–693)

Figure 14.16: Homogeneous Discrete Method

Figure 14.17: Inhomogeneous Discrete Method

The standard method of moments (SMM) is an efficient alternative to the discrete population balance approach. In this approach, the population balance equation is transformed into a set of transport equations for moments of the distribution. The ^th moment is defined by integrating the number density throughout the particle space weighted with the particle property raised to its ^th power. It is generally sufficient to solve only a few moment equations, typically three to six. This may provide a significant reduction in the number of equations to be solved compared with the discretized approach. Apart from the computational advantage, the SMM approach is useful when the entire distribution is not needed and certain average and total quantities are sufficient to represent the particle distribution. Typically, the zeroth moment represents the total number density, the second moment represents the total surface area per unit volume, and the third moment represents the total mass density.

In the SMM approach, no assumptions are made about the size distribution, and the moment equations are formulated in a closed form involving only functions of the moments themselves. However, this exact closure requirement poses a serious limitation, as aggregation (with the exception of the constant aggregation kernel) and breakage phenomena cannot be written as functions of moments.

The quadrature method of moments (QMOM) has a similar advantage as the SMM in terms of computational costs, but replaces the exact closure needed by SMM with an approximate closure. This allows application of QMOM to a broad range of applications without any limitations.