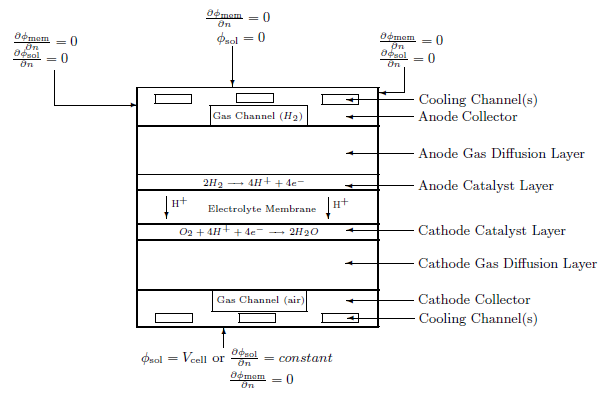
At the center of the electrochemistry is the computation of the rates of the anodic and cathodic reactions. The electrochemistry model adopted in Ansys Fluent is one that has been used by other groups ([325], [419], and [663]).

The driving force behind these reactions is the surface overpotential: the difference between the phase potential of the solid and the phase potential of the electrolyte/membrane. Therefore, two potential equations are solved for in the Fuel Cell and Electrolysis Model: one potential equation (Equation 20–64) accounts for the electron transport through the solid conductive materials and is solved in the TPB catalyst layer, the solid grids of the porous media, and the current collector; the other potential equation (Equation 20–65) represents the protonic (that is, ionic) transport of or and is solved in the TPB catalyst layer and the membrane. The two potential equations are as follows:

(20–64)

(20–65)

In the above equations, subscripts and refer to the membrane and solid phases, respectively.

The following figure illustrates the boundary conditions that are used to solve for and .

Figure 20.4: Boundary Conditions for the Electric Potential (Solid and Membrane) — PEM Fuel Cell

There are two types of external boundaries: those that have an electrical current passing through them, and those that do not.

As no ionic current leaves the fuel cell through any external boundary, there is a zero flux boundary condition for the membrane phase potential, , on all outside boundaries.

For the solid phase potential, , there are external boundaries on the anode and the cathode side that are in contact with the external electric circuit and only through these boundaries passes the electrical current generated in the fuel cell. On all other external boundaries there is a zero flux boundary condition for .

On the external contact boundaries, we recommend to prescribe fixed values for (potentiostatic boundary conditions). If the anode side is set to zero, the (positive) value prescribed on the cathode side is the cell voltage. Specifying a constant flux (say on the cathode side) means to specify galvanostatic boundary conditions.

The transfer currents, or the source terms in Equation 20–64 and Equation 20–65, are nonzero only inside the catalyst layers and are computed as:

The source terms in Equation 20–64 and Equation 20–65, also called the exchange current density (A/m³), have the following general definitions:

(20–66)

(20–67)

where
	= reference exchange current density per active surface area (A/m2)
	= specific active surface area (1/m)
	, = local species concentration, reference value (kmol/m3)
	= concentration dependence
	= surface overpotential (Volts) given by Equation 20–70 for the anode and Equation 20–71 for the cathode.
	= transfer coefficient (dimensionless)
	= Faraday constant (9.65x107 C/kmol)

The above equation is the general formulation of the Butler-Volmer function. Note that the effects of the number of electrons in electrochemistry reactions are accounted for in the transfer coefficients. A simplification to this is the Tafel formulation that reads,

(20–68)

(20–69)

By default, the Butler-Volmer function is used in the Ansys Fluent Fuel Cell and Electrolysis Model to compute the transfer currents inside the catalyst layers.

In Equation 20–66 through Equation 20–69, and represent the molar concentration of the species upon which the anode and cathode reaction rates depend, respectively. For PEMFC and SOFC, represents and represents . For Electrolysis, represents and is 1.0 (which indicates that the cathode reaction does not depend on any species concentration).

The driving force for the kinetics is the local surface overpotential, , also known as the activation loss. It is generally the difference between the solid and membrane potentials, and .

The gain in electrical potential from crossing from the anode to the cathode side can then be taken into account by subtracting the open-circuit voltage on the cathode side.

(20–70)

(20–71)

From Equation 20–64 through Equation 20–71, the two potential fields can be obtained.