During a simulation, Rocky solves the motion equations for every single particle,
updating its position and orientation in relation to a global reference frame. One of the
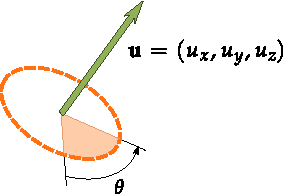
forms of representation that Rocky uses for describing mathematically the orientation of a
particle is the axis-angle formalism. In this kind of representation, the
orientation of a particle is defined by the orientation of an attached local frame of
reference which rotates an angle about an axis determined by a unit vector
, as illustrated in Figure 5.9: Axis-angle representation of a rotation in a 3D space..
For example, users must employ this representation for specifying the initial orientation
of a particle, when it enters the solution domain. Moreover, Rocky provides at output times
the instantaneous values of the components of the unit vector and the angle
, as particle properties. Using those values, magnitudes related to the
orientation of a particle can be precisely calculated as a post-processing operation. In order
to do that, it is useful to calculate the rotation matrix:
Where:
The effect of multiplying the rotation matrix by a vector expressed in the particle's local coordinates is to rotate that
vector the angle
around the axis defined by
. This operation, for instance, allows the coordinates that define the
geometry of a particle to be transformed to the global system of reference, with the
orientation defined by
and
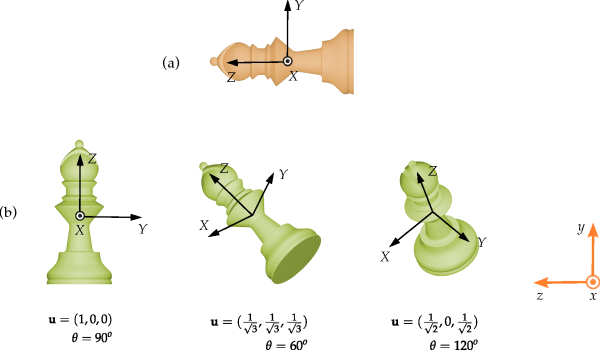
. As an illustration of this, Figure 5.10: Examples of the orientation of a particle represented with the axisangle formalism.(b) shows three
orientations of a particle in the global frame of reference, for three sets of values of
and
. Figure 5.10: Examples of the orientation of a particle represented with the axisangle formalism.(a) shows the same particle when the
orientation of the local frame of reference
XYZ coincides with the
orientation of the global frame
xyz.