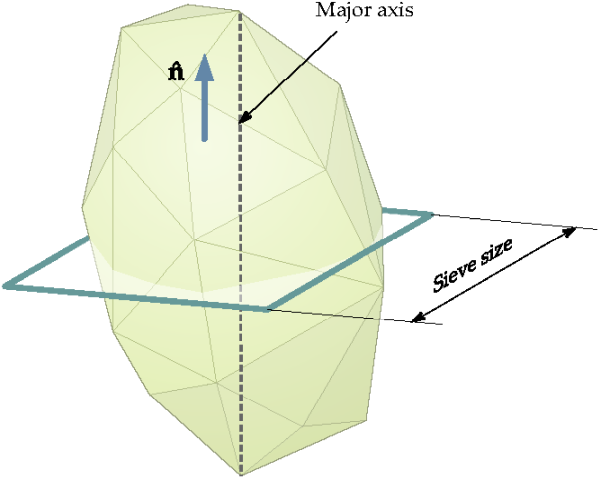
The sieve size of a particle is defined as the dimension of the smallest square aperture through which the particle can pass, as depicted in Figure 5.6: Sieve size of a polyhedral particle.. For polyhedral and custom solid particle shapes, Rocky uses an approximate method to estimate the sieve size.

Figure 5.6: Sieve size of a polyhedral particle.

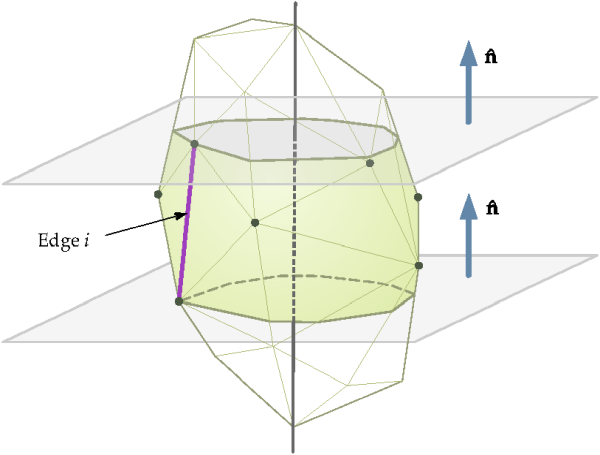
As a first step, the major axis of the particle is determined. In order to do this, all possible pairs of vertices on the particle's geometry are considered, looking for the two most distant vertices. In the algorithm implemented in Rocky, it is considered that the major axis of the particle will pass through those two vertices.

Figure 5.7: Example of a slice considered for determining sieve size candidates.

In the second stage of the algorithm, the largest particle dimension perpendicular to the major axis is sought. This will be the sieve size of the particle. In order to determine that, a sequence of slices of the particle's geometry is considered. As depicted in Figure 5.7: Example of a slice considered for determining sieve size candidates., each one of those slices is limited by two planes orthogonal to the major axis passing through the end points of an edge.

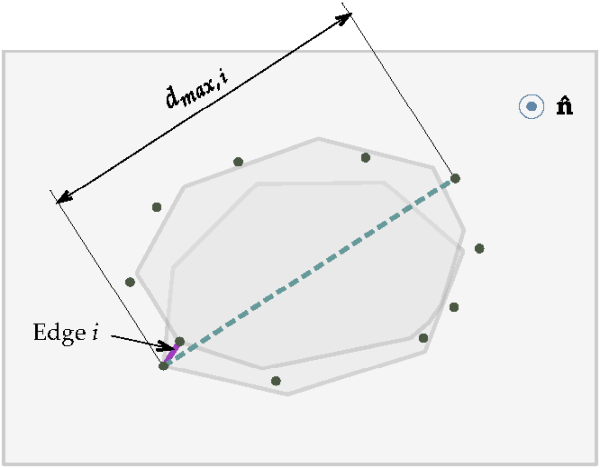
Then, all vertices contained between the two limiting planes are projected orthogonally onto any of those planes. The next step will be to determine the sieve size candidate associated to the slice. In order to do that, the distances between the projections of both vertices at the ends of the edge i and the projections of all other vertices are calculated. The sieve size candidate associated to the slice i will be the largest of those distances, , as depicted in Figure 5.8: Projection of the vertices onto an orthogonal plane to the major axis..

Figure 5.8: Projection of the vertices onto an orthogonal plane to the major axis.

In the end, the estimated sieve size will be the maximum value among the sieve size candidates determined considering the slices associated to all edges on the particle's geometry. That is:

(5–5)

The described algorithm works well for irregular particles, for instance, those representing rocks or rock fragments. For regular simple shapes, such as cubes or parallelepipeds, the algorithm usually will overestimate the sieve size.