Joint breakage models are used to determine if a joint between two elements in a flexible particle was loaded beyond its resistance capacity and, therefore, is no longer able to keep those elements joined. This type of discrete breakage differs from the instantaneous breakage models for non-flexible particles in that the resulting fragments can be only individual elements or groups of elements that originally made up a flexible particle. When a joint breakage model is active for a flexible particle group, every single joint in a flexible particle is evaluated for breakage. If after verifying the breakage criterion at a joint it is determined that it must fully break, the joint is deactivated and the previously joined elements become separate entities. In that way, if all joints in a flexible particle end up breaking apart, the number of resulting fragments will be the number of elements that originally formed that particle.

Figure 3.13: Vertices related to an undeformed joint between two elements of (a) a flexible fiber, (b) a flexible shell and (c) a flexible solid.

For the purpose of analyzing joint breakage only, the concept of joint vertex is considered in Rocky. These are the points where a joint breakage criterion is actually verified. The relative position of the joint vertices for the three types of flexible particles in Rocky is illustrated in Figure 3.13: Vertices related to an undeformed joint between two elements of (a) a flexible fiber, (b) a flexible shell and (c) a flexible solid.. The simplest case is that of fibers, in which there is only one vertex and it coincides with the joint's center point. For the joints in flexible shells, on the other hand, the two joint vertices initially coincide with vertices of the joined triangle elements. After the breakage of the joint starts, the position of those vertices may change, as will be described later on. Finally, as shown in Figure 3.13: Vertices related to an undeformed joint between two elements of (a) a flexible fiber, (b) a flexible shell and (c) a flexible solid.(c), the joint between two tetrahedral elements in a solid particle has initially three vertices, which coincide with vertices of those elements. However, if the joint breakage is partial, those vertices can be displaced and even more vertices can be generated in the joint. This process of partial breakage is described below.

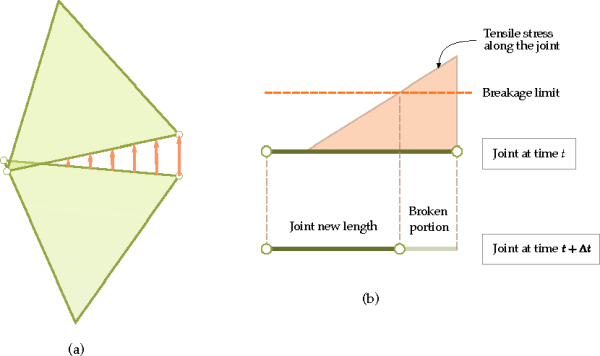
As only one vertex is associated to a joint in a fiber, when the criterion for joint breakage has been met at that point, the joint will break fully and instantaneously. On the other hand, joint breakage on shells and solid particles can be partial; consequently, a finite lapse of time can exist between the beginning of the joint breakage and the complete separation of the joined elements. The process of partial joint breakage is illustrated in Figure 3.14: Example of partial breakage of a joint in a flexible shell for a joint in a flexible shell. In this example it is assumed that the breakage criterion is based on a limit value for the tensile stress at the joint, although the process would be similar with other criteria as well.

Figure 3.14: Example of partial breakage of a joint in a flexible shell

In the general case, when both translational and rotational displacements of the joined elements are considered in conjunction, it is expected a linear variation of the stress along the joint, as depicted in Figure 3.14: Example of partial breakage of a joint in a flexible shell(a). If with a given deformation state all values of tensile stress become larger than the limit stress for breakage at the same time, the joint will fully break instantaneously. On the other hand, it is more likely to occur a situation as the one depicted in Figure 3.14: Example of partial breakage of a joint in a flexible shell(b), with the actual stress being larger than the limit stress only in a portion of the joint. This characterizes a partial joint breakage in Rocky.

As shown schematically in Figure 3.14: Example of partial breakage of a joint in a flexible shell(b), when the breakage criterion is satisfied only in a portion of the joint, Rocky will consider that only that portion breaks. For the subsequent time iterations, Rocky will recalculate the geometrical properties of the joint based on the new joint length. Moreover, the joint vertex adjacent to the broken portion will be relocated to the point where the actual stress is equal to the breakage stress limit. In following time iterations, the joint breakage is analyzed only in the remaining portion of the joint, reducing it further in portions where the breakage criterion is satisfied. This process continues until the joint length reduces to zero, at which point the joint is considered fully broken and it is then deactivated.

An equivalent partial breakage process is considered in solid flexible particles as well. The difference in relation to the previously described process for flexible shells is purely geometric. As shown in Figure 3.13: Vertices related to an undeformed joint between two elements of (a) a flexible fiber, (b) a flexible shell and (c) a flexible solid.(c), the joints in these types of particles have associated initially a triangular shape. When one of those joints is deformed, the distribution of stresses will be linear over that shape, possibly with stress values that exceed the breakage limit in a portion of it. Rocky will consider that this portion of the joint has broken and will remove it from the joint. Thus, the joint area will be reduced and the associated triangular shape will possibly be transformed into a quadrilateral. Further partial breakage events will reduce even more the joint area and transform its shape into an irregular polygon. In this process, more vertices at which the breakage criterion is verified will be added to the joint. As in the shell case, the geometrical properties of the joint will be recalculated at each partial breakage event. The described process will continue until the breakage criterion has been satisfied in the whole extension of the joint. At that moment the joint will be fully broken and, consequently, it will be disabled.

As shown in Figure 3.14: Example of partial breakage of a joint in a flexible shell, the determination of the stress variation along a joint in a flexible shell is made considering the instantaneous positions of the triangles located in the midplanes of the sphero-triangle elements. As these entities do not have thickness, the effect of the deformations associated to the bending around the first bending axis and the torsion are not taken into account in that calculation. As the stresses associated to those deformations are proportional to the shell thickness, which is usually much smaller than the size of the triangles, the influence of them on the breakage process is normally minor. However, Rocky users have now the option of including those deformations on the breakage calculations, if they consider it necessary. In order to do that, the checkbox Include Rotational Deformations must be turned on. In such case, the following stress is added to the tensile stress:

(3–34)

where:

Figure 3.15: Tensile deformation due to bending around the first bending axis, for a joint in a flexible shell

Similarly, the following stress related to the torsion deformation is added to the shear stress, if the breakage criterion is based on that stress component:

(3–35)

where:

When the checkbox is enabled for flexible fibers, the same additional stresses described above are considered. In that case, the expressions for calculating those stresses are the same of Equation 3–34 and Equation 3–35, replacing the shell thickness by the fiber diameter. On the other hand, for solid flexible particles, the linear deformations caused for all three angular deformations are always considered for the calculation of stresses, since in that case there is no internal simplification on the geometrical representation of the tetrahedral elements.

The following sections describe the joint breakage criteria currently implemented in Rocky.

 

3.4.1. Tensile stress criterion

When this criterion is selected, only tensile stresses at the joint will be verified in order to determine if a joint or a portion of a joint will break. The condition of breakage in this case can be expressed as:

(3–36)

where:

• is the joint normal stiffness per area unit, defined in section Linear elastic model.

• is the instantaneous displacement of a vertex of the joint, in the normal direction.

• is the tensile stress limit for joint fracture, which is a user input listed as Tensile Stress Limit in the Rocky UI.

Tensile stress criterion model is available in Rocky to either Straight or Custom Fiber and Custom Shell.

 

3.4.2. Shear stress criterion

In this criterion, only the shear stress generated at the joint is analyzed for determining if a joint or a portion of a joint will break. The shear stress criterion is formulated as:

(3–37)

where:

• is the joint tangential stiffness per area unit, defined in section Linear elastic model.

• is the instantaneous displacement of a vertex of the joint, in the tangential direction.

• is the shear stress limit for joint fracture, which is a user input listed as Shear Stress Limit in the Rocky UI.

Shear stress criterion model is available in Rocky to either Straight or Custom Fiber and Custom Shell.

 

3.4.4. Von Mises stress criterion

This criterion is formulated in terms of the von Mises stress, which is a scalar value of stress computed with the stress tensor components. Using the known forces at a joint vertex, this criterion can be expressed as:

(3–38)

where:

• and are the joint normal and tangential stiffness per area unit, respectively, defined in section Linear elastic model.

• and are the instantaneous displacements of a vertex of the joint, in the normal and tangential directions, respectively.

• is the von Mises stress limit for joint fracture, which is a user input listed as von Mises Stress Limit in the Rocky UI.

Von Mises stress criterion model is available in Rocky to either Straight or Custom Fiber and Custom Shell.