A flexible particle in Rocky can be thought of as a complex system with multiple modes of vibration. In general, the number of individual normal modes of vibration will be a multiple of the number of elements that make up the flexible particle. Each one of those vibration modes has associated a specific frequency, whose value will depend on various factors, such as the geometry and the material properties of the particle. When the motion of a flexible particle is locally perturbed by a collision, the resulting relative motion of the elements that form the particle can be considered as a superposition of the normal modes of vibration.
The joint damping forces and moments described in section Joint damping model are effective in reducing only the vibration modes of higher frequencies. Therefore, that approach will be successful in completely removing internal oscillations only when the number of elements forming the flexible particles is low. As the number of elements grows, it is common to observe that oscillations of low frequencies remain almost unaffected by the application of the joint damping. This may be unsuitable for some applications because usually those low-frequency oscillations are the most noticeable, as their amplitudes are larger than the ones of high-frequency oscillations.
In order to improve the capability of suppressing oscillations efficiently in all the frequency spectrum, Rocky 4.5 introduced a complementary damping option. This additional form of damping is named as element damping because damping forces are applied directly on each one of the elements forming a flexible particle. In this approach, an element damping force is defined by the expression:
(3–31) |
where:
is the translational velocity of the element e.
is the translational velocity of the parent particle that contains the element e.
is the element damping coefficient, which is defined later on in Equation 3–33.
Figure 3.12: Damping force proportional to the relative element velocity in relation to the parent particle's velocity.
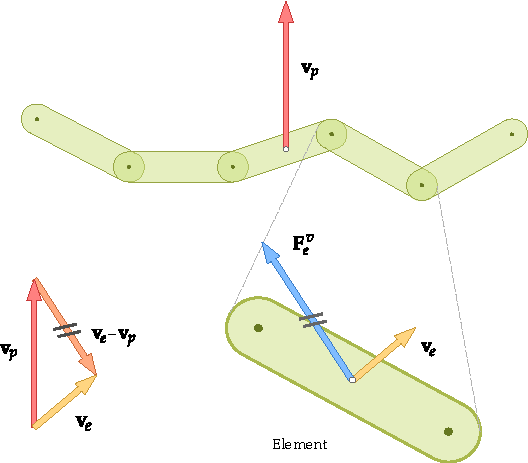
Figure 3.12: Damping force proportional to the relative element velocity in relation to the parent particle's velocity. illustrates how this force is related to the velocities and
. As a matter of fact, the difference
is actually the velocity of the element
relative to a frame of reference moving with the center of mass of the
parent particle. If that particle is moving as a rigid body, with all elements having the same
velocity, no damping force will be applied to the elements, according to Equation 3–31. On the other hand, when the particle collides and the velocity of
an element is perturbed, an element damping force will be applied opposing to the relative
velocity
at all times. Its net effect will be to reduce that relative velocity,
making the element velocity gradually approach the velocity of the parent particle. As time
passes, if no new perturbations arise, all elements of the particle will tend to move with the
same velocity, that is, the whole particle will tend to move as a rigid body again, without
internal deformations.
The velocity of the center of mass of the parent particle is defined as:
(3–32) |
where and
are the masses and velocities of the elements that make up the particle,
respectively.
The element damping coefficient is calculated in Rocky using the expression:
(3–33) |
where:
is the mass of the element
.
is the fundamental frequency of vibration of the whole particle, that is, the lowest frequency among all the frequencies associated to the vibration modes of the particle. Rocky will estimate this fundamental frequency based on the shape of the flexible particle and its physical properties.
is the element damping ratio, which is a user input listed in the Rocky UI as Damping Ratio | Element. It determines the intensity of the applied element damping, its allowed values are in the interval [0,1].
When both the joint and element damping are applied in conjunction, any internal oscillations in flexible particles will be removed some time after they were generated. The higher the values of the damping ratios, the faster the oscillations will be reduced after a collision. However, each type of damping can be applied also separately. As mentioned earlier, the joint damping will be effective in removing high-frequency oscillations, while the element damping will be more effective in the low-frequency range.


