The contact forces in any DEM code (including Rocky) consist of the following two parts:
Forces normal-to-contact plane
Forces tangent-to-contact plane
For spherical particles, the contact plane is perpendicular to the line that connects the centers of two spheres. In the case of particle-to-boundary contact, the line connects the center of a sphere and the closest point of a triangle making up a boundary. For non-round particles, the algorithm for determining a contact plane is more complex; it involves calculating one of any of the following:
The closest points of two particles.
The closest points of a particle and triangle.
The two points with the maximum overlap distance in the case of a physical contact.
The contact plane is a plane perpendicular to the line connecting these closest points. The descriptions for the normal and tangential force calculations used in Rocky, as well as the models used by these forces are presented below.
A normal force model for a DEM simulation has two major requirements. First, the force has to be a repulsive one. Second, the normal contact force model has to allow significant energy dissipation since a granular medium is an extremely dissipative system. A number of models have been proposed for these purposes. The models implemented in Rocky are discussed below.
This model, first proposed by Walton & Braun [19], was referred to as linear hysteresis model in previous versions of Rocky. This elastic-plastic (repulsive and dissipative) normal contact model allows simulation of the plastic energy dissipation on a contact without introducing the overhead of long simulation times.
In addition, since no viscous damping term is used, the energy dissipation is not dependent on the relative velocities of neighboring particles, making the energy dissipation insensitive to other contacts. An additional advantage of this model is that compressible materials can be accurately modeled due to the fact that the contact forces can be almost zero even at residual overlaps.
The hysteretic linear spring model is implemented in Rocky in an incremental way, as described by the following set of equations:
(2–1) |
(2–2) |
where:
and
are the normal elastic-plastic contact forces at the current time
and at the previous time
, respectively, where
is the timestep.
is the change in the contact normal overlap during the current time. It is assumed to be positive as particles approach each other and negative when they separate.
and
are the normal overlap values at the current and at the previous time, respectively.
and
are the values of loading and unloading contact stiffnesses, respectively.
is a dimensionless small constant. Its value in Rocky is 0.001. The part of the expression in which this constant is active ensures that, during the unloading, the normal force will return to zero when the overlap decreases to zero.
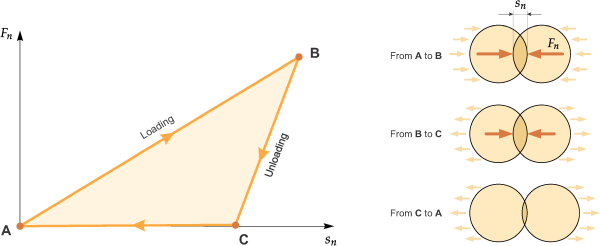
A typical cycle of loading/unloading is depicted in Figure 2.1: Schematics of a typical normal force-overlap response for the hysteretic linear
spring model..
Between points A and B, we have the loading process, in which the normal force overlap
increases linearly with slope . After reaching the maximum overlap, the unloading follows a steeper
line between points B and C, in which the slope is
. The plastic deformation for the contact only exists during the contact,
so any residual deformation is forgotten after the contact ceases. The energy dissipated
in the collision is numerically equal to the shaded area in the force-deformation diagram
of Figure 2.1: Schematics of a typical normal force-overlap response for the hysteretic linear
spring model..
Figure 2.1: Schematics of a typical normal force-overlap response for the hysteretic linear spring model.
The loading and unloading stiffnesses are defined by the particle size, the bulk
Young's modulus, and by the restitution coefficient of contacting materials, the last two
of which the user inputs into Rocky. The coefficient of restitution in Rocky is a measure of energy dissipation for the contacting pair of
materials. For the contact of two particles, or of a particle with a boundary, the loading
and unloading equivalent stiffnesses are defined, respectively, as:
(2–3) |
(2–4) |
where subscripts 1 and 2 identify the two contacting particles. The individual stiffnesses associated to a particle and to a boundary are computed, respectively, as:
(2–5) |
(2–6) |
where:
is the particle material's bulk Young's modulus or elastic modulus, which the user can input in the corresponding material's editor panel. Note : A value of
for the particle bulk Young's modulus is a reasonable number for most particle sizes.
is the boundary material's Young's modulus, which is also a user input.
is the particle size.
In long-term contacts, for instance, among particles in a stockpile, the hysteretic linear spring model can give rise to oscillations of very small amplitudes on the normal force and on the overlap. Although these oscillations are barely noticeable, this phenomenon can prevent the particles from reaching a state of absolute repose. Because of this, an additional mechanism of energy dissipation was introduced in Rocky, in order to dissipate spurious oscillations in long-term contacts. Note that this force does not act during regular collisions, therefore, the energy dissipation specified by the restitution coefficient will not be altered at all by this force on those collisions. This mechanism consists in the addition of a viscous force which is only activated during secondary loading cycles on long-term contacts. That additional force is defined in a similar fashion to that of the dissipative part of the contact force on the Equation 2–8 model:
(2–7) |
where is the time derivative of the normal overlap and
is the damping coefficient, defined as in Equation 2–10.
The value of the damping ratio
needed in that equation can be specified by the user in the
Advanced sub-tab of the Solver panel, in which
it is listed as Damping Ratio for Hysteretic Linear Spring Model.
Allowed values for this parameter are in the range from 0 to 1. Note that the higher the
value of the damping ratio, the faster will be the dissipation of oscillations.
Two models of tangential forces are compatible with the hysteretic linear spring model: the Linear spring Coulomb limit model model and the Coulomb limit model model. Moreover, it works only with two built-in adhesive models in Rocky: the Constant adhesive force model model, and the Linear adhesive force model model.
The linear spring-dashpot model was referred to as linear elastic viscous model in previous versions of Rocky. This phenomenological model, first proposed in the seminal paper of Cundall & Strack [24], is widely used in DEM, mainly because of its simplicity. The normal contact force in this model is composed of a linear elastic repulsive force and a damping force, that is:
(2–8) |
where:
is the normal contact stiffness, defined previously for the linear hysteretic spring model in Equation 2–3.
is the normal damping coefficient.
is the contact normal overlap.
is the time derivative of the contact normal overlap.
The energy dissipation in the linear spring-dashpot model is viscous in nature and
due exclusively to the damping force term in Equation 2–8. The value of
the normal damping coefficient can be determined in a way that the viscous energy dissipation matches
the energy dissipation of an inelastic collision, determined in turn by the value of the
coefficient of restitution. In order to do that, the damping coefficient is defined in
Rocky as follows:
(2–9) |
where:
is the damping ratio, a dimensionless parameter whose value is related to the restitution coefficient (see below).
is the effective or equivalent mass for the contact, defined as:
(2–10)
where
and
are the masses of the contacting particles, whereas
is the mass of the particle in contact with a boundary.
In general, there will be one value of the damping ratio for which the energy dissipation on a collision event modeled with the
linear spring-dashpot will replicate the energy dissipation predicted by the coefficient
of restitution. Note that the coefficient of restitution is considered in Rocky to be a
property of the interaction between two materials. The functional relationship between the
damping ratio and the coefficient of restitution, derived from that condition, is:
(2–11) |
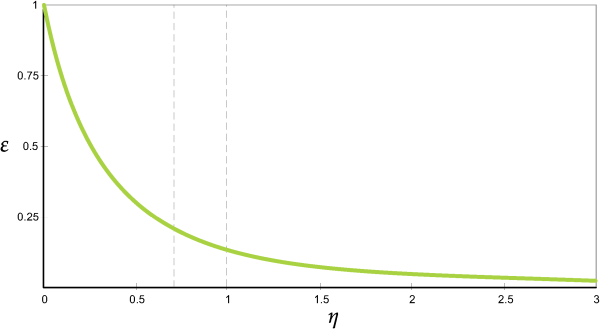
As can be seen in Figure 2.2: Graph of the relationship between the damping ratio
and the restitution coefficient
., Equation 2–11
defines the restitution coefficient
as a monotonic function of the damping ratio
. Since the inverse of this function cannot be determined analytically,
Equation 2–11 is solved numerically in Rocky in order to find the value
of
that corresponds to the value of
prescribed by the user.
Equation 2–11 was derived originally by Schwager & Poschel [17], considering that the end of a collision happens when the contact
normal force decreases to zero. It is common in DEM to see the use of a simpler expression
for the relation between and
, derived from the condition that the end of a collision occurs at a
later time, when the deformation returns to zero. It is easy to show, however, that the
normal force given by Equation 2–8 turns negative at that time. Since a
negative normal contact force is an attractive one, the assumption of a purely repulsive
contact force is contradicted by that practice. On the other hand, Equation 2–11 is totally consistent with that assumption and for that reason it
was adopted in Rocky.
Although the linear spring-dashpot model is popular in DEM formulations, it tends to be less accurate than the hysteretic linear spring model because energy dissipation in the real world is plastic rather than viscous. Its accuracy drops especially when particles have simultaneous multiple contacts, since the amount of viscous dissipation is accurate only for single contacts.
The linear spring-dashpot model works with the constant adhesive force model and the linear adhesive force model, as well as the linear spring Coulomb limit model and the Coulomb limit model for tangential forces.
The Hertzian spring-dashpot model is similar to the linear spring-dashpot model. The main difference is that both the elastic and the damping components of the normal force are nonlinear functions of the overlap in the Hertzian model. The elastic part is based in the classical contact theory developed by Hertz in the late nineteenth century [25].
The form of the Hertzian spring-dashpot model implemented in Rocky can be written as:
(2–12) |
in which the stiffness coefficient is defined as:
(2–13) |
where:
is the reduced Young's modulus, defined by the expression
(2–14)
in which
and
are the Young's moduli of the two contacting particles or the particle and the boundary, depending on the contact type. Moreover,
and
are the respective Poisson's ratios.
is the effective or equivalent radius, defined by the expression:
(2–15)
in which
and
are the sizes of the contacting particles in a particle-particle collision, whereas
is the size of the particle in a particle-boundary collision.
Following the practice proposed initially by Tsuji et al. [18], the damping coefficient for the Hertzian model in Rocky is defined in a similar fashion as for the linear spring-dashpot model:
(2–16) |
where is the effective mass, defined previously in Equation 2–10, and
is the damping ratio for the Hertzian spring-dashpot model. Antypov
& Elliott [23] demonstrated that considering appropriate
variable transformations, the solution for a movement equation based on the Hertzian model
can be mapped onto the solution of an equivalent equation based on the linear
spring-dashpot model. That equivalence is possible only if the damping coefficient for the
Hertzian model is defined as:
(2–17) |
where is the same damping ratio used in the linear spring-dashpot model. In
Rocky, the value of
is determined solving and then using the resulting value in to obtain
. This guarantees that no matter whether the linear spring-dashpot or the
Hertzian model is used, the viscous energy dissipation in a collision event is equal to
the one specified through the coefficient of restitution.
The Hertzian spring-dashpot model works with all three models available for tangential forces, namely, the linear spring Coulomb limit model, the Coulomb limit model, and the Mindlin-Deresiewicz model. Moreover, it works with all built-in adhesive models in Rocky, namely the constant adhesive force model, the linear adhesive force model, and the JKR adhesive force model.
The models used in Rocky to calculate the tangential components of the contact forces are described below.
The tangential force in this model is elastic-frictional. If the tangential force were
considered purely elastic, its value at time would be given by:
(2–18) |
where:
is the value of the tangential force at the previous time. Note that the minus sign in this equation arises from the fact that the tangential force always opposes to the tangential displacement.
is the tangential relative displacement of the particles during the timestep.
is the tangential stiffness defined as:
(2–19)
where
is the loading normal stiffness defined in Equation 2–3 and
is a user-defined parameter listed as Tangnetial Stiffness Ratio in the corresponding materials interaction editor panel.
In this model, however, the tangential force cannot exceed the Coulomb's limit. Therefore, the complete expression for the tangential force is:
(2–20) |
where:
is the contact normal force at time
.
is the friction coefficient, defined as:
(2–21) |
in which and
are, respectively, the static and the dynamic friction coefficients.
These are properties that the user can define in the corresponding materials interaction
editor panel in Rocky.
The sliding is considered to be taking place on the contact the first time the
magnitude of the tangential force exceeds the limit of
. Once that force falls below the value of
, the contact is considered non-sliding again.
This tangential model works with all three normal contact models in Rocky.
This is the simplest tangential force model implemented in Rocky. The tangential force according to this model is given by:
(2–22) |
where:
is the friction coefficient defined in Equation 2–21.
is the normal force at the contact.
is the tangential component of the relative velocity vector.
The condition of sliding considered for this model is based on the tangential component
of the relative velocity. If that component is below , the contact is considered non-sliding. In the current version of Rocky,
the value of
is set to 0.001 m/s.
The Coulomb limit model works with all three types of normal forces models, i.e., the Hysteretic linear spring model model, the Linear spring-dashpot model model and the Hertzian spring-dashpot model model.
This model is new to Rocky as of v4.1. The tangential force in this model is given by the expressions:
(2–23) |
(2–24) |
where:
is the friction coefficient, defined in Equation 2–21.
is the normal force.
is the tangential relative displacement at the contact.
is the tangential component of the relative velocity at the contact.
is the maximum relative tangential displacement at which particles begin to slide.
is the effective mass, defined in Equation 2–10.
is the tangential damping ratio, which is estimated in Rocky by means of:
(2–25)
where
is the coefficient of restitution for the respective materials interaction.
The value of the maximum relative tangential displacement is determined in Rocky using the expression:
(2–26) |
where:
and
are the Poisson's ratios of the two particles or the particle and the boundary, depending on the contact type.
is the normal overlap.
It is worth noting that when , the parameter
turns to zero in Equation 2–24. It is easy to show that the magnitude of the
tangential force reduces to
in that case, and, therefore, the Mindlin-Deresiecz model becomes
equivalent to the Coulomb limit model under that specific condition.
The Mindlin-Deresiewicz model works only with the Hertzian spring-dashpot model. Moreover, the Mindlin-Deresiewicz model does not work properly with any rolling resistance model for shaped (non-spherical) particles. This is due to a known issue that can cause instabilities in the angle of repose. Therefore, when this model is selected in a problem with shaped particles, the rolling resistance must be disabled in the project.