The normal contact models described in section Normal force models are appropriate for simulating non-adhesive and dry granular materials. Unfortunately, quite often granular materials can have various moisture contents that can cause them to adhere to themselves and other surfaces with which they come into contact. In order to capture this behavior, the repulsive normal force has to be supplemented by the attractive normal force to accurately predict its flow characteristics. For example, this is required for wet and sticky materials where the adhesion is from liquid bridge forces or other mechanisms.
One important point to note is that cohesion/adhesion of a bulk solid is a function of the stress. The linear force adhesion contact model in Rocky captures this physical phenomenon by scaling the cohesion/adhesion with the force of contact.
With proper calibration the constant adhesive force model can be used to simulate the behavior of adhesive materials that do not exhibit stress consolidation effects, e.g., when adhesion is due to liquid bridge forces.
Note: In this version of Rocky, a liquid bridge model is provided via an external Module. Refer to the Rocky Module Manual for details.
This is the simplest adhesion model in Rocky and is described by the equation:
(2–27) |
where:
is the normal adhesive contact force.
is the contact normal overlap.
and
are the mass of the particles in contact.
is the gravity acceleration.
is a model parameter listed as in the Rocky UI Adhesive Distance. If the distance between two particles or between a particle and a boundary surface is below
, the adhesive force will be activated. In Rocky, the value of this parameter can be defined in the materials interaction editor panel.
is a model parameter listed in the Rocky UI as Force Fraction. The value of the adhesive force will be equal to the particle gravity force multiplied by the value of
. If the force fraction is 1, that means the adhesive force will be equal to the gravity force on the particle. In the case of contact between two particles of different mass, the smallest mass is considered for gravity force calculations.
The constant adhesive force model works with all three types of normal force models in Rocky, including the Hysteretic linear spring model model, the Linear spring-dashpot model model and the Hertzian spring-dashpot model model.
Like the constant adhesive force model, the linear adhesive force model requires calibration of the material behavior. This model is appropriate for granular materials with stress consolidation.
The linear adhesive force model as implemented in Rocky can be described by the following expression:
(2–28) |
where:
is the normal adhesive contact force at the current time.
is the contact normal overlap at the current time. It is assumed to be positive when the colliding entities touch each other, and negative when they are separate but close. In this latter case, its absolute value will give the separation distance between those entities (two particles or a particle and a boundary surface).
is a model parameter listed as in the Rocky UI Adhesive Distance. The adhesive force between two neighboring entities will be greater than zero if and only if the separation distance between them is less than the value of
.
is a model parameter listed as in the Rocky UI Stiffness Fraction. This parameter is defined as the ratio of the adhesive stiffness to the contact loading stiffness.
is the loading contact normal stiffness defined in Equation 2–3.
The linear adhesive model, in essence, behaves like an attractive linear spring. When
two neighboring entities are separate but close, the adhesive force is zero if the actual
distance between them is larger than the adhesive distance. When that threshold is passed
and the entities get closer, the adhesive force increases proportionally to the difference
between the adhesive distance and the actual separation distance. If physical contact is
reached, the adhesive force increases further, this time proportionally to the sum of the
adhesive distance and the overlap. The coefficient of proportionality is defined in both
cases as the adhesive stiffness, given by .
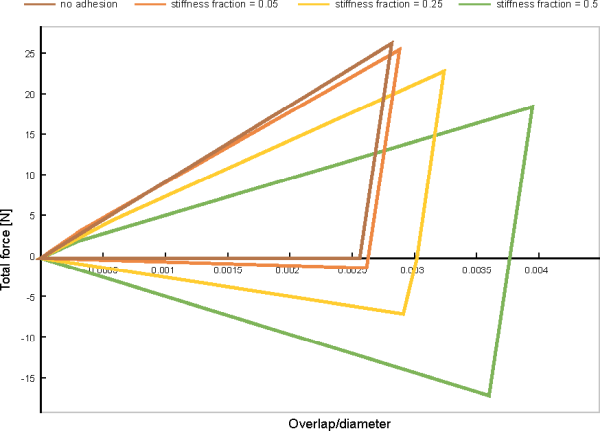
Figure 2.3: Examples of force-overlap plots for different adhesive stiffness fractions. shows some examples of the force-overlap response of a particle collision with a wall, for both dry and adhesive impacts. The hysteretic linear spring model is used as normal contact force in all cases, and the stiffness fraction varies from 0 to 0.5, for the linear adhesion model. It is evident that the larger the contact overlap, the larger the attractive force, therefore allowing an accurate model to represent the stress consolidation of granular materials.
The linear adhesive model works with all three types of normal force models in Rocky, including the Hysteretic linear spring model model, the Linear spring-dashpot model model and the Hertzian spring-dashpot model model.
The Johnson-Kendall-Roberts[13], JKR, model introduces the effect of adhesion into the Hertzian contact model. In the JKR model, the contact area between two particles is slightly larger than the one predicted by the Hertzian theory. This is the result of a surface energy term that is added to the total energy of the system.
The adhesive part of the normal force when the JKR model is employed is given by:
(2–29) |
where:
is a model parameter listed as Surface Energy in the Rocky UI. The value of this parameter can be introduced in a materials interaction editor panel.
is the effective Young's modulus, defined in Equation 2–14.
is the radius of contact between particles or between a particle and a boundary.
The contact radius is related to the normal overlap by means of the expression:
(2–30) |
where is the effective particle radius, defined in Equation 2–15.
For a given normal overlap , is solved in Rocky to determine the corresponding value of
, in order to calculate the adhesive force using Equation 2–29.
When the JKR model is enabled, the elastic part of the Hertzian normal force must be
corrected, because the contact radius in the JKR model is different from the radius
predicted by the Hertzian model. The corrected elastic force, expressed as a function of the
radius of contact , is given by:
(2–31) |
The JKR model has a strong theoretical basis and is widely accepted for adhesive elastic spheres. Since the surface energy can be measured experimentally, this model could be used without calibration, in principle, for simulating perfect spheres. In any other case, calibration still will be needed. In Rocky, the JKR adhesive force model only works with the Hertzian spring-dashpot model model.