Rocky includes models for predicting the instantaneous breakage of particles based upon the stressing energy involved in collisions with walls or other particles. These models work only with polyhedral convex particles. Therefore, spherical, rounded and concave shapes, as well as rigid fibers and shells, are not able to break in Rocky when using these models. An important common characteristic of all these breakage models is that when a particle breaks, the resulting fragments preserve both mass and volume.As the instantaneous breakage is based on the impact energy, which is the energy accumulated during loading in a collision, the period in which the overlap increases, there is no possibility of having viscous dissipation on the contacts when particle mass is decreasing (fragment is formed). If the dissipation is based on outdated (non-broken) mass, it will create an instability. If it is based on fragment mass, it will generate fictitious energy in the system. The only feasible normal force modelwith non-viscous dissipation is Hysteretic Linear Spring.
Users can override the default calculation of the impact energy with a custom module. For more details, please refer to the Rocky API Solver Manual.
The impact energy is used in Rocky as the main input parameter for the built-in instantaneous breakage models; therefore, users will need to implement a custom impact energy calculation only if they intend to use a custom contact force model along with such breakage models.
Even in that case, users may choose not to implement the calculation of the impact energy. Rocky will use in such situation a standard calculation based on the impact work, as defined in Equation 4–10.
The Ab-T10 breakage probability is based on the model posed by Vogel & Peukert [1] and the subsequent modification proposed by Shi & Kojovic [2]. This breakage model treats every particle as a single entity that can be broken into fragments instantaneously based upon the impact energy it receives.
In Rocky, the specific impact energy, , is computed by summing the work done by the contact forces at all contact
points in a particle during the loading period. In order to damage the particle,
should be greater than the minimum breakage energy of the particle,
. This minimum breakage energy is related to the particle size through the
expression:
(2–38) |
where:
is the reference minimum specific energy value for a reference particle size of this material. This parameter is referred to as Reference Minimum Specific Energy in the Rocky UI.
is the reference particle size, referred to as Referece Size in the Rocky UI.
is the actual particle size.
In order to take into account the damage caused by successive collisions, the
verification of breakage is made by considering a cumulative value of the specific impact
energy, . If
is the instantaneous value of the specific impact energy at a given time
during a loading phase, the value of
will be updated only if
and
, where
is the maximum value of impact energy registered on the particle until the
last time in which the value of
was updated. During reloading periods in collisions with complex loading
cycles, the second condition ensures that impact energy values below
are not taken into account more than once as cause of damage. When those
conditions are satisfied, the update is made according to the expression:
(2–39) |
where is the specific impact energy at the previous timestep. Whenever the
particle is unloaded and the value of
decreases below
, the value of
is reset to zero, so a new cycle of loading may begin, in which the value
of
will be able to increase again.
In the Ab-T10 model, the breakage probability for a given cumulative specific contact energy value is calculated as:
(2–40) |
where:
is a material constant referred to as Selection Function Coefficient in the Rocky UI.
A particle will break if at any moment the value of computed with Equation 2–40 is larger than the strength
of the particle. When that condition is met and the particle breaks, the fragments are
generated following the Voronoi fracture algorithm according to a size distribution that the
user specifies. Two options are currently available: Gaudin-Schumann and Incomplete beta function. For either option, the value of the necessary
parameter is calculated according to the expression:
(2–41) |
where:
is the percentage of fragments passing a screen size of 1/10th of the original particle size
.
is the maximum
for a material subject to breakage, referred to as Maximum t10 Value in the Rocky UI.
New fragments generated by breakage can break further if they are subjected to
additional damage, generating even smaller fragments. In order to prevent existing contacts
at the moment of the breakage to have an abnormal influence on the subsequent breakage of
newly generated fragments, the update of using is skipped during a certain number of timesteps after a breakage
event. Currently, that number of timesteps is set to 25 in Rocky.
For more information about the Ab-T10 breakage model, please refer to the papers of Potapov & Donahue [3] and Shi & Kojovic [2].
This model is based on the PhD work of Prof. L. M. Tavares [7] at the University of Utah and the further development with his research group at the Federal University of Rio de Janeiro, Brazil. The Tavares model extends the functionality of simpler breakage models by adding capabilities that can make breakage prediction quite realistic in a wide variety of situations. In particular, the model is useful in describing ore degradation during handling as well as size reduction in different types of crushers, providing greater confidence in predicting both the proportion of broken particles and product size distribution.
In the Tavares breakage model, the breakage probability is based on an upper-truncated
log-normal distribution of the specific fracture energy, . This distribution is defined by the expression:
(2–42) |
where:
is the relative specific fracture energy, defined below in Equation 2–43.
is the median particle specific fracture energy.
is the variance of the log-normal distribution of fracture energies. This is a model parameter that must be specified by the user, in the Rocky UI it is listed as
.
The relative specific fracture energy is defined as:
(2–43) |
where corresponds to the specific impact energy above which all particles would
break in a single impact. In the Rocky UI, the value of
is specified indirectly through the ratio
, listed as
.
The particle specific fracture energy is highly dependent on the particle size, . This dependency is introduced in the model by means of the following
correlation between the median specific fracture energy,
, and the particle size [6]:
(2–44) |
where ,
, and
are model parameters that should be fitted to experimental data. These
parameters are listed in the Rocky UI as
,
, and
, respectively.
Whenever a particle enters the solution domain in Rocky, a random strength is assigned
to it. This property can be interpreted as the value of at which it will break during a simulation. Then, considering Equation 2–42--Equation 2–44, it can be determined the
corresponding value of
, the specific fracture energy of the particle. Here, this specific
fracture energy will be denoted as
, because this value is considered to determine if the particle will break
during the first collision event. The exact criterion considered for the particle breakage
will be described below.
Every time a particle undergoes a collision event, the fracture specific energy will decrease due to the accumulated damage to the particle during the loading process. Therefore, after every new loading cycle without breakage, a new particle specific fracture energy is computed based on the previous one and on an estimation of the accumulated damage during the loading. The mathematical expressions considered for this are [7]:
(2–45) |
(2–46) |
where:
is the particle specific fracture energy after
loading cycles without breakage. Therefore,
may be interpreted as the value of
computed at the end of the previous loading cycle.
is the fractional damage in the particle during the
th loading cycle.
is the damage accumulation coefficient, a model parameter listed as
in the Rocky UI.
is the instantaneous specific impact energy in the particle at the end of the
th loading cycle.
Let's define as the instantaneous specific impact energy at a given time
. In Rocky, that instantaneous impact energy is computed by taking into
account the work done by all contact forces acting on the particle at that time. This
includes the work done by elastic and dissipative normal forces, as well as the work done by
elastic tangential forces.
Now, let's consider that a particle is in its th loading cycle. Whenever the value of
is greater than
, that is, the specific fracture energy at the end of the previous loading
cycle, the particle will break. If the unloading of the particle begins before that breakage
condition is satisfied, a new value of specific fracture energy may be computed with Equation 2–45 and Equation 2–46. This new threshold value for
breakage in a subsequent loading cycle is calculated whenever
decreases in the unloading below
, which is the minimum specific energy for breakage. This is a user input
parameter, listed in the Rocky UI as e min.
When a particle breaks, the geometries of the resulting fragments are generated by
means of the Voronoi fracture algorithm, according to a size distribution specified by the
user between the two options available: Gaudin-Schumann and incomplete beta function. The value of the parameter, needed in either of those distributions, is calculated
according to the expression:
(2–47) |
where:
is the percentage of fragments passing a screen size of 1/10th of the original particle size
.
and
are model parameters listed as A and b', respectively, in the Rocky UI.
is the value of the specific impact energy at the instant of breakage.
is a measure of the specific fracture energy of the broken particles.
Regarding the specific fracture energy in Equation 2–47, two alternatives are currently
available in Rocky. The first one is to use the value of the current specific impact energy
at the instant of breakage,
. As this term will cancel out with the numerator in Equation 2–47, with this option the value of
will become independent of the specific impact energy of the broken
particle. In the Rocky UI, this option is provided via the Energy for t10
Calculation parameter, and is listed as Current Particle
Energy(the default option).
The second option available is to use the value of the median specific fracture energy
of the broken particles , defined as [7]:
(2–48) |
This option is listed as Median Specific Fracture Energy (e50b) in the Rocky UI.
As was the case with the Ab-T10 model, some preventive measures are also taken in order to avoid excessive re-breakage of fragments resulting from previous breakage events. First, in order to rule out any influence of existing contacts on the breakage of new fragments, calculations of damage are skipped during 25 timesteps after the breakage event that produced them. Second, in order to reduce the available energy for damaging newly formed fragments, a parameter listed as Fragments Energy Factor was introduced into the modeling. The value defined for this parameter will multiply the value of the instantaneous specific contact energy when considering the breakage criterion for fragments.
For more information about the Tavares breakage model, please refer to the papers previously cited and also to Tavares & King [8], and Carvalho & Tavares [5].
Besides the mechanisms of breakage based on fracture energy described in previous sections, particles may also break in Rocky when its deformation exceeds a certain preset value. This additional mechanism is introduced in order to prevent some artifacts related to low-stiffness particles that can experience large overlaps during a simulation.
This additional breakage mechanism is activated by default in Rocky, but users may disable it if necessary through the option Set Breakage Overlap Factor, which is found in the Advanced sub-tab of the Solver panel. When this option is enabled, users will be able to set a value to the Breakage Overlap Factor. From that point onward, the value of the ratio of the overlap to the minimum fragment size will be monitored for every contact in the simulation. Whenever that ratio exceeds the value of the Breakage Overlap Factor, the Rocky solver will perform one of two possible actions. If the related particle or fragment is large enough so that its breakage is possible, it will be broken at once. On the other hand, if breakage is not possible because the size of the particle or fragment is too close to the minimum fragment size, it will be removed from the simulation. The minimum fragment size is a user input listed as Minimum Absolute Size on the Breakage | Fragment Distribution sub-tab of the particle group being specified.
Note: The particle or fragment will be removed if its volume is smaller than 3 times the volume of the smallest fragment allowed in a simulation.
When a particle breaks because of a large overlap, the resulting fragment size
distribution is determined according to the same model chosen for the primary breakage
model. If necessary, the value of the parameter is computed with the respective value of impact energy at the
moment of breakage.
Regardless of the type of instantaneous fragmentation model that is selected, once the particle reaches the breakage point, Rocky generates fragments preserving both the total particle mass and volume, using one of the available distribution models.
In general, the number and size of fragments will be dependent upon the particle?s
original size, on the value of the parameter, and the value of the minimum admissible fragment size.
This last parameter is controlled by two user inputs, listed in the Rocky UI as Minimum Absolute Size and Minimum Absolute Size Ratio , respectively. The first one allows users to specify the minimum absolute size in absolute terms, whereas the second does it in relative terms. The minimum absolute size allowed for fragments in Rocky will be the largest value between the Minimum Absolute Size value and the product of theMinimum Absolute Size Ratio and the size of the particle or fragment being broken in the breakage event. When generating the fragments at a breakage event, no fragment is allowed to have a size smaller than the resulting value from that operation.
Allowing the generation of too small fragments would be inadvisable mainly because the computation time may increase beyond reasonable limits. The reason for this is twofold: the total number of objects that must be tracked in the simulation may grow exponentially, whereas the timestep may need to be reduced significantly in order to keep the simulation process stable.[1] A side effect of limiting the minimum absolute size of fragments is that the actual size distribution satisfies the prescribed size distribution[2] only for fragments larger than approximately 2.5 times the specified minimum absolute size.
In the same line of preventing the generation of too small fragments, an additional safeguard parameter is defined as the Minimum Volume Fraction for Fragment Disabling. When a generated fragment is detected to have an actual volume smaller than the value of that parameter multiplied by the minimum volume allowed for a fragment, such fragment is removed from the system.
The full fragment size distribution is determined from the value of by assuming a Gaudin-Schumann distribution with unitary slope:
(2–49) |
where:
is the cumulative percentage of the mass of passing fragments.
is the screening sieve size.
is the size of the broken particle.
The full fragment size distribution is determined from the value of by assuming an incomplete beta function distribution:
(2–50) |
where:
is the percentage of fragments passing a screen size of
th of the original size
.
and
are model parameters fitted to experimental data. In Rocky, the user can introduce values for these parameters, corresponding to different values of
, in a table provided in the corresponding data editor panel.
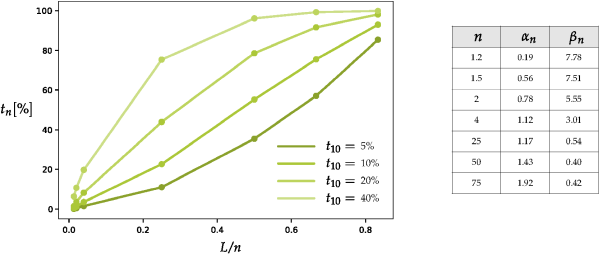
Figure 2.4: Examples of fragment size distributions for different values of . shows examples of fragments size distributions
obtained with parameters fitted to experimental data for limestone [5]. Marker points in the plot correspond to values computed with Equation 2–50,
using the values of
and
reproduced in the same figure. In Rocky, intermediate values of the
fragment size distribution are determined by means of linear interpolation of the values
computed with Equation 2–50.