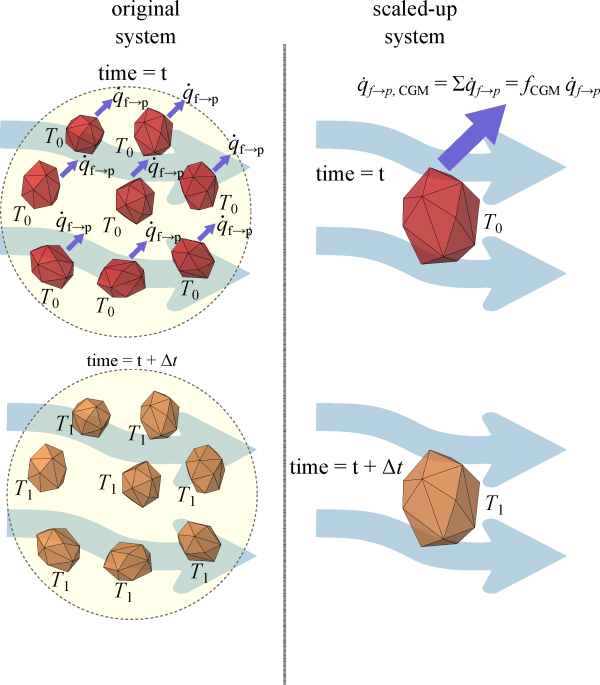
In cases with heat transfer between particles and fluid, the constraint to the Coarse Grain Model is to keep keep the same temperature variations in the scaled system as in the original system. Figure 5.3: The heat exchange conserves the temperature variations of the original system when using CGM. shows a collection of particles, initially at a temperature T₀ exchanging heat with the surrounding fluid. After a time interval of , the particles reach the temperature T₁. The scaled-up system should have this same temperature, therefore ensuring the same energy transfer between fluid and particle phase. The used in this example is 2.

Figure 5.3: The heat exchange conserves the temperature variations of the original system when using CGM.

As can be seen in Figure 5.3: The heat exchange conserves the temperature variations of the original system when using CGM., in a similar fashion to the fluid forces, the total heat transfer rate due to convection on the parcel should be equal to the heat transfer rate due to convection on a single original particle times the number of particles the parcel represents, .

Corrections are needed for convection heat transfer rate given by Equation 4–2 for performing the correct scaling on the convective heat transfer rate for CGM. As the , is equal to times the area of the original particle, , a single is sufficient to reach the desired scaling. Equation 5–3 shows the final form of the convective heat transfer rate for parcels when CGM is used.

(5–3)

A single scale-factor is necessary because the area of the parcel, , is equal to times the area of the original particle,, so this final addition is sufficient to reach the desired scaling.

Finally, the convective heat transfer coefficient calculated for the scaled-up system must be the same as for the original system, computed as Equation 4–3. For this purpose, as the particle size is scaled up by , the fluid thermal conductivity must also be scaled by , as shown in Equation 5–4.

(5–4)

The Nusselt number, , is obtained from correlations. These correlations are functions of the Reynolds and Prandtl numbers and of the local volume fraction of particles. Since the Reynolds number was already modified due to the drag calculation, as shown in Equation Equation 5–2, the additional parameters are not changed when using the CGM model.