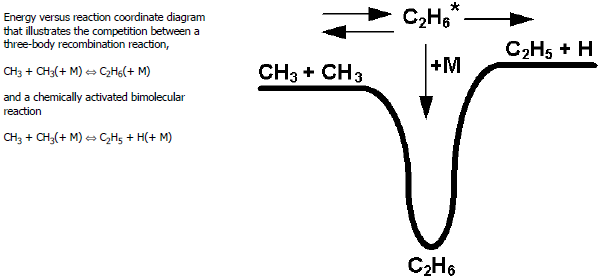
As an example of a chemically activated bimolecular reaction, consider the
reaction . This reaction, which is endothermic, occurs through the same chemically
activated
adduct as does the recombination reaction
. Figure 3.2: Energy versus reaction coordinate diagram
helps to illustrate the
competition between these alternative channels using a reaction-energy diagram. As the
pressure increases, deactivating collisions of
with other molecules cause the rate coefficient for
formation to increase. At the same time, these deactivating collisions
preclude the dissociation of
into
, thus causing this rate coefficient to decrease with increasing
pressure.
We assume the rate coefficient for a chemically activated bimolecular reaction to be described by the following function:
(3–36) |
where is analogous to the Lindemann form of Equation 3–27
. Note that in Equation 3–36
,
is the pressure-independent factor, whereas in Equation 3–27
it is
. The three choices for the
function are exactly the same as for the unimolecular fall-off reactions,
that is, the Lindemann (
), Troe, or SRI forms.
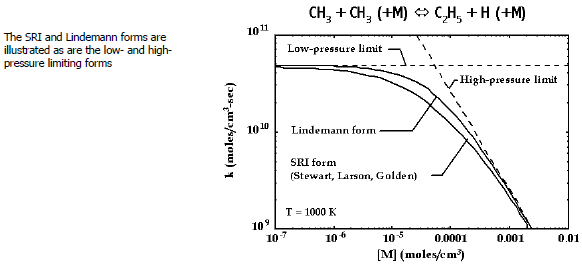
Figure 3.3: Rate constant as a function of pressure at fixed temperature for a chemically activated reaction
illustrates the rate-expression
behavior for the example chemically activated reaction, . Both the Lindemann and the SRI formulations are shown, as well as the
high- and low-pressure limiting cases. The specific constants for the SRI form
(
,
,
,
,
,
,
,
,
) are taken from Stewart, Larson, and Golden.[18]
For this example, note that the units for
are cm3 /(mole ⋅ sec),
are cm3 /(mole ⋅ sec), and
are 1/sec. The limiting cases are recognized easily from the behavior of
Equation 3–36
. In the low-pressure limit,
,
, causing the pressure-ratio factor in Equation 3–36
to approach unity. Hence,
, that is, a pressure-independent function. In the high-pressure limit,
,
and
.
Figure 3.3: Rate constant as a function of pressure at fixed temperature for a chemically activated reaction