Note: The DDES and SDES models are not available in CFX.
The main practical problem with the DES formulation (both for
the Spalart Allmaras and the standard SST-DES model) is that there
is no mechanism for preventing the limiter from becoming active in
the attached portion of the boundary layer. This will happen in regions
where the is less than the boundary layer thickness.
In this case, the flow can separate as a result of the mesh spacing
(mesh-induced separation), which is undesirable. The
DES formulations
reduce the impact of the DES term inside the boundary layer. This
is achieved by function
, which protects the boundary layer. For
, the original SST
model is recovered; for
, the original DES model is utilized.
(2–195) |
There are several historic formulations for the function
.
Originally, the
and
blending
functions of the SST model were used [56]. Later, a specifically tuned function
termed
was added [226].
(2–196) |
Where is the wall distance,
is the von Karman constant, and
.
is superseded by the Shielded DES function
(SDES). The
function offers essentially asymptotic
shielding under mesh refinement and is recommended (and also set as
the default). This function is unpublished and proprietary to Ansys.
In addition, the SDES model features an alternative definition of the mesh length scale:
(2–197) |
where is
the volume of the cell and
is its maximum edge length. Finally, for
SDES, the model coefficient is reduced to
. Both of these changes result in much reduced eddy
viscosity levels in detached shear layers and quicker "transition"
from RANS to LES.
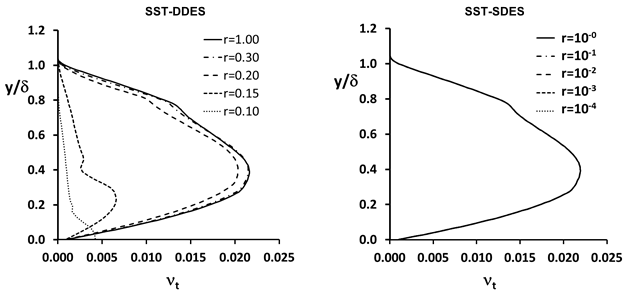
Figure 2.2: Eddy viscosity profiles for DDES and SDES models under mesh
refinement shows the effect of improved
shielding on boundary layer flows. The parameter is the local ratio of grid
spacing,
, to boundary layer thickness,
. The grid spacing is
for the DDES model and
for the SDES model. Note, in the figure, that the
range of
is much wider for SDES. Nevertheless, the SDES model
is able to preserve the RANS model eddy viscosity whereas the DDES
model deteriorates for values of
.