Aqwa-Line does not evaluate drag forces on submerged components. AqwaWave therefore allows Morison forces on such components to be calculated and added to the incident and diffracted wave forces from Aqwa-Line.
Two types of component are considered here:
Relatively large diameter tubular components simulated using facets in Aqwa-Line, but for which drag loads are considered important (for example, GBS shafts)
Smaller diameter tubular members subject to drag and inertia loads (for example, conductor framing on GBS). Although provision is made for modeling the inertia loads on such tubes in Aqwa-Line, this is not the recommended modeling for AqwaWave, and the tubular members do not need to be modelled in Aqwa-Line.
When evaluating Morison loads on such components of the structure, several factors need to be considered:
The incident flow is expected to be modified by the presence of the main structure due to diffracted wave forces. The particle velocities and accelerations on which the Morison forces are based need to consider this effect.
The local water surface during the passage of a wave is also expected to be modified due to the presence of the structure, therefore affecting the extent of structure subjected to wave loading. A ‘caisson effect’ (overall increase in water height) and a ‘ride up’ on vertical members cutting the surface are expected.
The effects of current velocity on drag should be considered. Current velocities should also be modified to allow for the presence of the structure.
Although linear wave theory is considered sufficient for evaluating incident and diffracted wave effects, this is often not sufficient for drag loads near the water surface where the particle velocities and water surface elevation can often be in excess of that predicted by simple Airy theory. Some consideration should be given to the effects of higher order wave theory.
The method of modeling of the structure should be considered. Although the application of drag and inertia loads to tube elements is relatively straightforward, some further rule must be provided to assign pressures to tubular structures defined by plate or solid elements.
The above considerations are addressed in the following two sections under the headings of Fluid Flow and Load Application.
At any point in the flow outside the Aqwa facet model, the incident and diffracted wave flow potential can be calculated using the same Green’s function routines as Aqwa-Line. The rate of change of potential in each principal direction gives the velocity of the flow for that direction. The effect of all contributing facets is considered. These can be added as a vector to the incident flow to give the disturbed flow around the structure. Water particle accelerations are derived simply from the rate of change of velocity.
A current profile (variation of current with depth) may be specified in the AqwaWave data for each wave case and phase selected from the Aqwa-Line analysis. The current flow is assumed to be horizontal, but the direction may vary with depth. For each given point, a current velocity is then calculated by linear interpolation to the required depth. This velocity is again summed as a vector to the wave velocity in the disturbed flow, calculated as above. The user-defined current profile is assumed to include the effects of the structure disturbing the flow. The program does not modify the current velocities as it does for waves. Principles of momentum preservation or even runs of Aqwa-Line with the current represented as a long duration wave may be helpful in determining this modified profile.
Flow around a massive object tends to cause a local distortion of the still water surface known as a ‘caisson effect’ and water tends to ‘ride up’ members that cut the water surface. The latter effect is normally not considered to significantly change global load on the structure, but is of some importance to local design, particularly wave slam, slap and the determination of the required air gap. The ‘caisson effect’ is significant on GBS type structures and can result in the total load being applied higher up in the structure. AqwaWave calculates most of this effect, which is due to the diffracted wave. (The increase in wave elevation due to diffraction may be obtained explicitly, using the field point facility in Aqwa-Line. The pressure at a given point at the still water level may be obtained using this method and the dynamic displacement of the water surface may be derived from the simple h = p/(ρg) formulation.)
The effect of this artificial raising of the water surface is simply to increase (or decrease if negative) the extent of structure subject to water pressure loads. If a positive value is found, the undisturbed water-surface motions are assumed to apply over the increase in depth. Otherwise, the motions are cut off at the reduced water surface.
Higher order wave theory may produce higher loads than simple Airy theory and typically account for a raising of the water surface elevation at the crest and a smoothing of the trough. Although not dealt with explicitly by AqwaWave, you can attempt to model the effect by inputting a scaled-up wave height, obtained using a suitable scaling factor. It is suggested that an estimate for this factor be obtained from a program that does allow for different wave theories, such as Ansys Mechanical.
Small diameter tubular members are handled as below:
The water surface elevations at the ends of the element are evaluated with due allowance for the local increase or decrease mentioned above.
If both ends of the element are below the water surface, then the member is fully loaded.
If neither end of the element is below the water surface, then the member is unloaded.
If only one end of the element is in the water, the member is loaded over the wetted length only.
The fluid flow at each end of a loaded length is evaluated in accordance with Fluid Flow.
The fluid flows at each loaded end are transformed into loads per unit length perpendicular to the member using Morison’s equation as below:
Where:
F = the force per unit length
Cd = the drag coefficient
ρ = the mass density of water
D = the member diameter
u = the instantaneous velocity resolved normal to the member
Cm = the inertia coefficient
A = the cross-sectional area = πD2/4
a = instantaneous acceleration resolved normal to the member
Note: Cm = 1 + Ca
Where
Ca = the added mass coefficient.
The added mass can be ignored by setting Cm to zero. However, if Cm is set to a value less than one, but not zero, a negative Ca will be used as the Cm = 1 + Ca relationship is respected, hence the valid values for Cm are 0 or ≥1.
You should take into account marine growth when inputting the diameter into the AqwaWave data. The drag and inertia coefficients can be defined explicitly by you for all tube elements in the structural model. Members with no coefficients will not be considered. The coefficients occur in the AqwaWave data and are referenced by the structural element.
Note:
Distributed loads on the element are written to the output data file as SFBEAM surface loads.
You must not define either OFFSETS or LOCAL AXES for pipe or beam elements in the structural model.
Large Aqwa substructures, which have cylindrical symmetry (such as the shaft of a GBS) and which have been modelled in Aqwa-Line using panel elements can also have their drag loads calculated by AqwaWave. Such substructures are referred to here as ‘Aqwa components’.
Ignoring current for the moment, the flow ‘seen by’ an Aqwa component, at any instant of time, is taken to be the flow which, at that instant, is being exactly cancelled (normal to every plate) by the combined flow due to all the hydrodynamic sources on the component. The flow ‘seen by’ the component can therefore be calculated by adding, to the incident flow (assumed undisturbed), the flow due to all the hydrodynamic sources on the whole Aqwa structure, except those on the component. The resulting flow is evaluated on the central axis of the component and (after adding the constant current) used in Morison’s equation to calculate the drag.
AqwaWave has no knowledge of what constitutes an Aqwa component. If it is required to calculate the drag on such a component, all the elements which constitute the component must be specified in the AqwaWave data (see OMIT command Assignment Data - ASGN), so that the corresponding hydrodynamic sources can be OMITTED from the drag calculations.
Two cases need to be considered:
The tubular shaft is represented by tube elements in the structural model.
The tubular shaft is represented by solid or shell elements having a wetted surface.
Forces on a tube element idealisation of these shafts may now be calculated exactly as before, except that inertia loading is not generally required and should be prevented by setting Cm to zero.
Shell or solid element models require more data. Such elements should be arranged into groups, each of which represents a ring of elements. The end co-ordinates, diameter and drag coefficients for each such ring are given in the AqwaWave data. Rings are referenced by group number in the AqwaWave data.
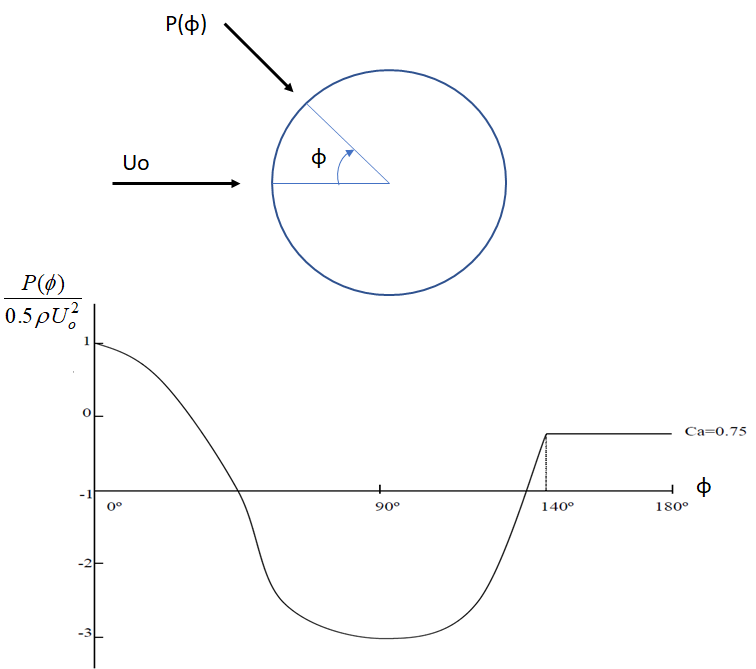
With two ends, a diameter and a drag coefficient, each ring can now be handled exactly as for the above tubes as far as the evaluation of distributed loads on the length of the tubular element. The distributed loads (which vary from end to end) now need to be assigned as pressure loads on to the wetted faces. Fortunately, there is ample literature to show the likely distribution of drag pressure around such a cylinder, and a pressure distribution as illustrated in Figure 2.2: Varitaion of Drag Pressure Around a Cylinder.
The coordinates of each node at each element of the ring are found and transformed relative to the start and end of the tube it represents. From this, a pressure can be derived according to the calculation shown at the beginning of this section.
The drag loads on the tubular elements and the pressures on the elements of the rings are evaluated as above and are summed with incident/diffraction loads calculated in accordance with the previous section, Incident, Diffracted, and Radiated Wave Forces, prior to being written to the output structural data file in the appropriate format.
It should be noted that the above treatment of the water surface elevation and linearization of pressure loads is relatively simplistic. Excessive errors will occur if the element mesh is too coarse, particularly near the water surface. This should be considered when meshing the model.