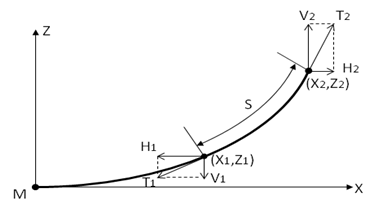
Each catenary segment in Aqwa is considered to be uniform. As the solution of the catenary equations is well documented (for example, as described in [4]) a summary of the solution is presented in this manual.
The equations can be expressed in a mooring
local axis system Mxyz, whose local x-axis is a projection on to the
sea bed of the vector joining the two attachment points and whose
z-axis points vertically upwards. At the origin the catenary line
profile has zero slope, i.e. , as shown in Figure 9.6: Catenary Solution.
For a catenary which has zero slope at the contact/attachment point on the sea bed these equations can be written as
(9–25) |
where is the unstretched suspended length
from the origin to the attachment point
(for a given tension force
at the point
, for
instance at the fairlead),
is the submerged weight per unit length, and
is the stiffness per unit length.
The stretched length of the suspended catenary line is
(9–26) |
When the unstretched length of a catenary
segment from its top right end is
, where
is shorter than the theoretical
unstretched suspended length
, and the tension force at the top right end is known,
the position of the bottom left end of this segment is
(9–27) |
The horizontal and vertical components of the tension at the left-hand end are
(9–28) |
The stretched length of this catenary segment is
(9–29) |
The extension of this segment is
(9–30) |