Position, velocity, acceleration and force are represented in Aqwa by vectors with both magnitude and direction. These vectors can be described in the different coordinate systems by means of an axis transformation.
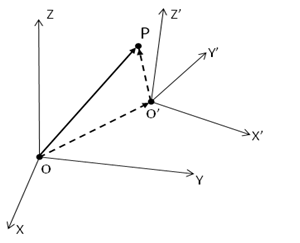
Figure 1.3: Axis Transformation shows two coordinate systems, the origin of the O'X'Y'Z' frame is at [X0, Y0, Z0 ] T in the OXYZ frame, where the superscript T denotes a matrix transpose. The directional cosines of the O'X'Y'Z' axes relative to the OXYZ axes are written as
(1–1) |
If the coordinate of a point is represented as [X, Y, Z] T in OXYZ and [x, y, z] T in O'X'Y'Z', then we have
(1–2) |
where is the transformation matrix.
To transfer [X, Y, Z] T in OXYZ into a coordinate in the O'X'Y'Z' frame, we have
(1–3) |
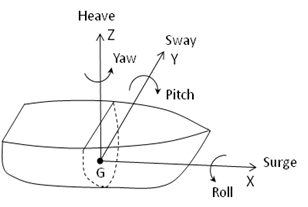
Employing the conventional seakeeping notation of a floating rigid body (see [40]), motions of that body are defined as the translational movements of the center of gravity and rotations about a set of orthogonal axes through the origin of GXYZ, as illustrated in Figure 1.4: Floating Rigid Motions . This intermediate coordinate system moves with the mean forward speed of the vessel but its X-, Y-, and Z-axes remain constantly parallel to the corresponding X-, Y-, and Z-axes of the fixed reference axes.
- Translations
u1 = surge (along X)
u2 = sway (along Y)
u3 = heave (along Z)
- Rotations
= roll (about X)
= pitch (about Y)
= yaw (about Z)
The naming of the various motions assumes that the body is described such that the forward and aft direction is parallel to the X-axis. If the body lies parallel to the Y-axis, then the rolling of the body will be termed 'pitch' and the pitching termed 'roll'.
For large amplitude rotational motion analysis, determination of Euler angles is a necessary step in kinematics and model graphic presentation. Aqwa defines the orientation of a structure using Euler angles. These are the rotation angles about the three axes of GXYZ:
A rotation of about the X-axis:
(1–4) |
A rotation of about the Y-axis:
(1–5) |
A rotation of about the Z-axis:
(1–6) |
The Euler rotation matrix is defined as a sequence of three rotations, in the order of the rotation first about the X-axis of GXYZ, then the Y-axis, and finally the Z-axis of GXYZ. It can be represented as the matrix product:
(1–7) |
With this Euler rotation matrix, similar to Equation 1–2, the position of a point in the fixed reference axes can be expressed as
(1–8) |
where (Xg, Yg, Zg ) T is the coordinate of the center of gravity in the fixed reference axes and (x, y, z) T is the coordinate of this point in the local structure axes (LSA).
As a special case when all the rotational angles are small,
for instance , the
Euler rotation matrix can be simplified to:
(1–9) |
where