Benchmark C2

VMC2
Elliptic Membrane Under a Uniformly Load

Overview

Reference:

J. Barlow, G. A. O. Davis, "Selected FE Benchmarks in Structural and Thermal Analysis", NAFEMS Rept. FEBSTA, Rev. 1, October 1986, Test No. LE1 (modified)

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Element Type(s):

2D 4-Node Structural Solid Elements (PLANE182)

2D 8-Node Structural Solid Elements (PLANE183)

Input Listing:

vmc2.dat

Test Case

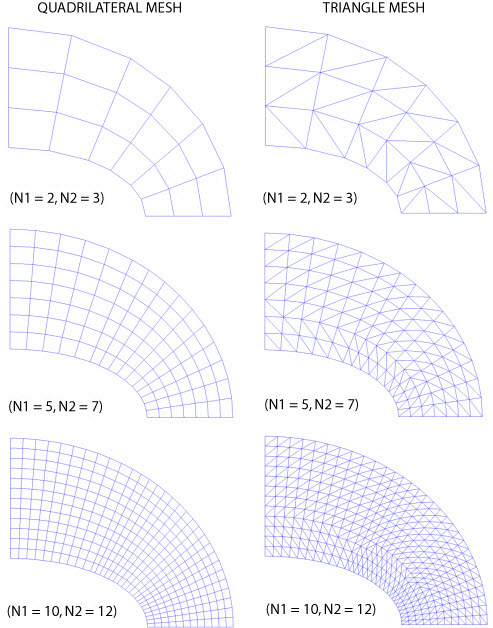
An elliptic membrane structure of thickness t is subjected to a uniformly distributed outward pressure P. Monitor the tangential edge stress σ_y at target point 1 for a series of uniform mesh refinements using quadrilateral and triangular elements. Compare the effect of increased mesh refinement with the percent energy error norm.

Figure 589: Elliptic Membrane Problem Sketch

Material Properties

Geometric Properties

Loading and Boundary Conditions

E = 210 x 10³ MPa

υ = 0.3

a = 1.75 m

b = 1.0 m

c = 2.0 m

d = 1.25 m

t = 0.1 m

Parameter Definitions

N1 = no. elements in circumferential direction, per area

N2 = no. elements in radial direction per area

At x = 0 UX = 0

At y = 0 UY = 0

Along outer edge P = -10 MPa

Figure 590: Representative Mesh Options

Results Tables

Target Solution: SY = 92.7 MPa Results Comparison - Quadrilateral and Triangle Meshing

ETYP	N1	N2	DOF	% Error Norm	SY Ratio
182	2	3	56	31.557	0.489
182	5	7	256	19.057	0.712
182	10	12	806	12.022	0.817
182	2	3	56	26.575	0.861
182	5	7	256	14.197	0.987
182	10	12	806	8.290	1.012
183	2	3	182	10.657	0.837
183	5	7	930	2.665	0.942
183	10	12	3050	1.159	0.973
183	2	3	146	5.764	0.899
183	5	7	720	0.981	0.963
183	10	12	2330	0.270	0.982

Assumptions, Modeling Notes, and Solution Comments

From an element performance standpoint, the problem is designed to test membrane elements for accurate modeling of the strain variation, nodal stress extrapolation, and curved boundary modeling (of higher order elements).
From a modeling standpoint, the problem is designed to test quadrilateral and triangular meshes for solution accuracy with various element types. For the areas modeled, all exterior line segment specifications for mesh density are made equal for the various mesh options.
For quadrilateral and triangle element meshes under uniform mesh refinement (parameters N1 and N2 varied), the calculated percent error in energy norm follows a log-log linear relationship to the number of degrees of freedom in the model. The higher order element (PLANE183) exhibits nearly identical log-log slopes while the lower order element (PLANE182) exhibits a more gradual slope. These results illustrate that the PLANE183 solutions converge at nearly the same rate under uniform refinement while PLANE183 converges at a slower rate. The percent error in energy norm results indicate that global accuracy is best obtained by PLANE82 for any given DOF set. However, the σ_y stress at target point 1 shows that for uniform refinement, PLANE182 gives better results (at that point) under moderate mesh refinement. A fine mesh using PLANE183 in place of a coarse mesh of PLANE183 may produce better localized stress values.