VM72

VM72
Logarithmic Decrement

Overview

Reference:	W. T. Thomson, Vibration Theory and Applications, 2nd Printing, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1965, pg. 45, ex. 2.3-1.
Analysis Type(s):	Mode-Superposition Transient Dynamic Analysis (ANTYPE = 4)
Element Type(s):	Combination Elements (COMBIN40)
Input Listing:	vm72.dat

Test Case

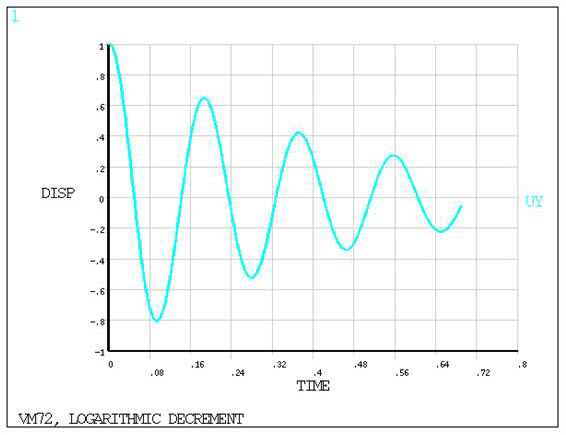
Determine the damped natural period τ_d and the ratio R between any two successive amplitudes of the freely vibrating spring-mass-viscous damping system. The system is initially held at rest at the stretched position Δ and then released.

Figure 98: Logarithmic Decrement Problem Sketch

Material Properties

W = 10 lb

k = 30 lb/in

c = 0.12 lb-sec/in

Δ = 1 in

g = 386 in/sec²

Analysis Assumptions and Modeling Notes

The node locations are arbitrarily selected. The initial static force is k Δ = 30 lb and the mass is m = W/g = 0.02590673 sec²/in². The integration time step (0.003 sec) is based on 1/60 of the period to allow the step changes in acceleration to be followed reasonably well and to produce sufficient printout for the theoretical comparison. Almost 4 cycles are included in the 0.0 to 0.69 sec time range. A static solution is done at the first load step. POST26 is used to get a displacement versus time display.

Results Comparison

Peak Number[1]	1	2	3	4
Max. Amplitude, in	1.0000	0.64981	0.42306	0.27525
Time, sec	0.0000	0.18600	0.37200	0.55800

Sequence number of the positive displacement vibration amplitude peaks

	Target	Mechanical APDL	Ratio
R_1-2	1.5350	1.5389	1.003
R_2-3	1.5350	1.5360	1.001
R_3-4	1.5350	1.5370	1.001
Damped natural period_1-2	0.18507	0.18600	1.005
Damped natural period_2-3	0.18507	0.18600	1.005
Damped natural period_3-4	0.18507	0.18600	1.005

Figure 99: Displacement vs. Time Display