VM71

VM71
Transient Response of a Spring-Mass-Damper System

Overview

Reference: W. T. Thomson, Vibration Theory and Applications, 2nd Printing, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1965, pg. 41, ex. 2.2-1.
Analysis Type(s): Mode-Superposition Transient Dynamic Analysis (ANTYPE = 4)
Element Type(s): Combination Elements (COMBIN40)
Input Listing: vm71.dat

Test Case

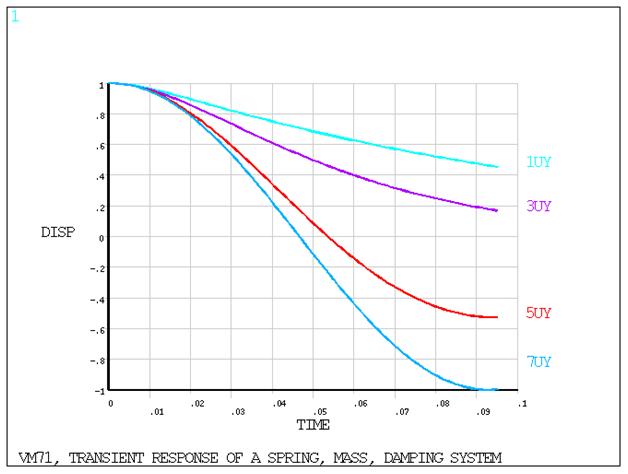
A spring-mass system with viscous damping is displaced by a distance Δ and released. Determine the displacement u at time t for four damping ratios:

  • ξ = 2.0

  • ξ = 1.0 (critical)

  • ξ = 0.2

  • ξ = 0.0 (undamped)

Figure 96: Spring-Mass-Damper System Problem Sketch

Spring-Mass-Damper System Problem Sketch

Material PropertiesLoading
w = 10 lb
k = 30 lb/in
m = w/g = 0.02590673 lb-sec2/in
Δ = 1 in
g = 386 in/sec2

Analysis Assumptions and Modeling Notes

The initial static force is calculated as kΔ = 30 lb and the damping coefficients are calculated as c = 2ξsqrt(km) = 3.52636, 1.76318, 0.352636, and 0.0 lb-sec/in for the four damping ratios (ξ) given in the test case, respectively. The node locations are arbitrarily selected. The integration time step (0.001 sec) is based on 1/180 of the period to allow the step changes in acceleration to be followed reasonably well and to produce sufficient printout for the theoretical comparison. The maximum time of 0.095 sec covers about 1/2 the period. A static solution is done at the first load step. POST26 is used to extract results from the solution phase.

Results Comparison

t = 0.09 secTargetMechanical APDLRatio
u, in (for damping ratio = 2.0)0.474200.476371.005
u, in (for damping ratio = 1.0)0.189980.192451.013
u, in (for damping ratio = 0.2)-0.52108-0.519510.997
u, in (for damping ratio = 0.0)-0.99688-0.994980.998

Figure 97: Displacement vs. Time Display

Displacement vs. Time Display