VM73
VM73
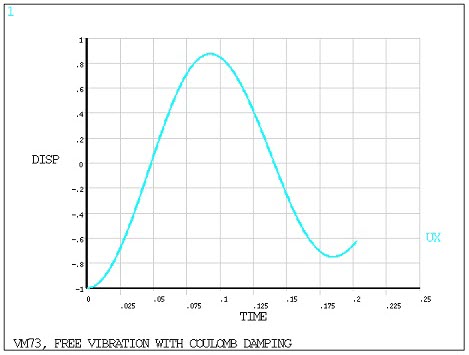
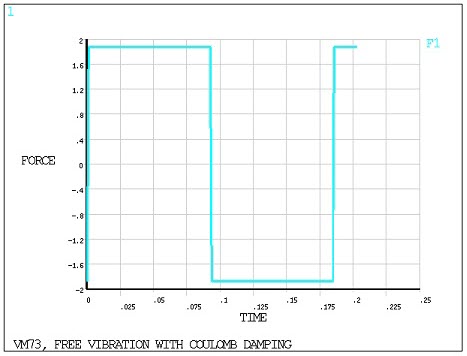
Free Vibration with Coulomb Damping
Test Case
A spring-mass system with coulomb damping is displaced a distance Δ
and released. Dry friction is assumed to act as a limiting sliding
force F between the sliding mass and the surface. Determine the displacement
u at various times t.
Analysis Assumptions and Modeling Notes
One combination element is used with the slider in parallel
with the spring. The slider spring constant (k1 = 10,000 lb/in) is arbitrarily selected high enough to minimize
the elastic contact effect but low enough to also allow a practical
integration time step size. The integration time step (0.2025/405
= 0.0005 sec) is based on
1/Nf where
N = 20 and f is the system natural frequency. At release, the mass
acceleration is not necessarily zero. Therefore, a load step with
a small time period is used to ramp up to the appropriate acceleration
while maintaining an essentially zero velocity. The final time of
0.2025 sec allows one full cycle of motion. POST26 is used to postprocess
results from the solution phase.
