VM320
VM320
Nonlinear Harmonic Analysis of a Frictional Damper
Overview
| Reference: | Guillen, Jerome. (1999). Studies of the dynamics of dry-friction-damped blade assemblies (HAL Id: tel-00365016) [Doctoral dissertation, University of Michigan]. HAL Archives-Ouvertes. |
| Analysis Type(s): | Harmonic Analysis (ANTYPE = 3) |
| Element Type(s): |
Spring-Damper Elements (COMBIN14) Structural Mass Elements (MASS21) 3D Node-to-Node Contact (CONTA178) |
| Input Listing: | vm320.dat |
Test Case
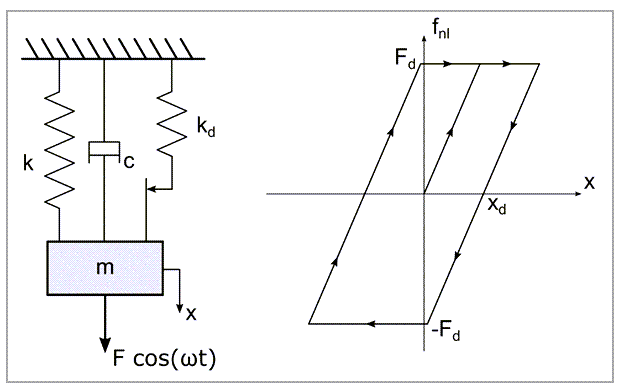
A single-DOF linear spring-mass-damper system is linked to a frictional damper following an elastic Coulomb's friction law, whose hysteresis curve is shown in Figure 585. The mass is excited with a harmonic force so that the equation of motion is expressed as:
(320–1) |
with the nonlinear frictional force defined by:
(320–2) |
| Material Properties | Loading |
|---|---|
|
m = 944.6 kg c = 7700 kg/s k = 2.4 107 N/m kd = 2.4 107 N/m Fd = 246.048 N |
F = 0.5 Fd |
Analysis Assumptions and Modeling Notes
The linear oscillator is defined using COMBIN14 and MASS21 elements and constrained to move along the UX direction. The frictional damper is modeled by a node-to-node contact element CONTA178, having normal and tangential stiffnesses equal to kd. The constant normal force is prescribed by defining an initial penetration equal to Fd/kd, and the sliding force Fd is enforced by defining a friction coefficient μ=1.
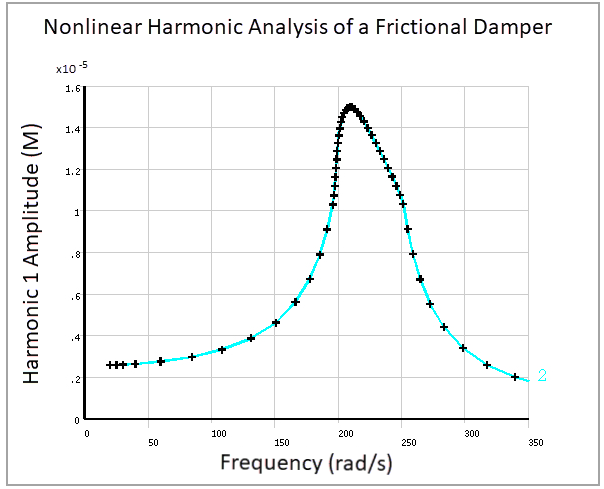
The model is solved using the harmonic balance method with one harmonic (HROPT,HBM,1) on a frequency range from 20 to 350 rad/s. Appropriate displacement and frequency scaling factors of 10-5 and 200 respectively are applied to improve the convergence rate.
The amplitude of the first harmonic of the displacement is obtained for each calculated frequency.