Overview

Test Case

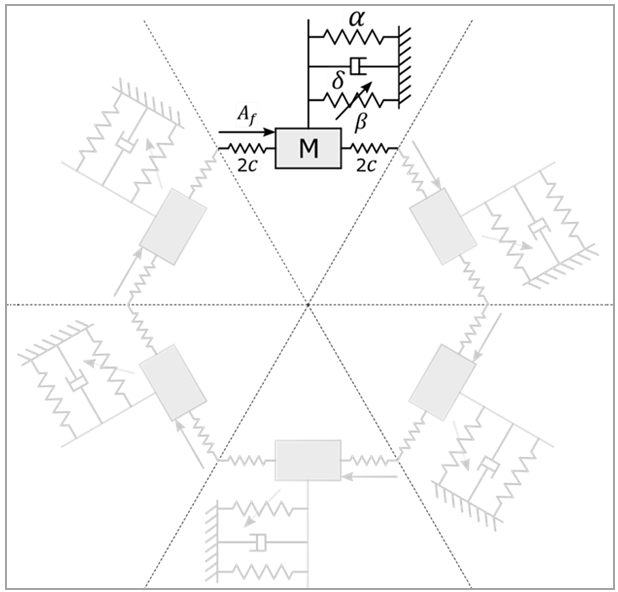
As shown in the figure below, a disk with blades that can undergo large deformation is approximated by a cyclic chain of six linear-cubic oscillators linked by linear springs. A harmonic force is applied on each sector so that each oscillator is governed by the following equation:

(319–1)

where is the displacement of the k^th oscillator and is the excitation frequency. The parameters are defined in the following table.

Figure 582: Cyclic Chain of Six Linear-Cubic Oscillators

Analysis Assumptions and Modeling Notes

Only one sector is modeled, and cyclic constraint equations on the low and high edges of the sector are created with the multistage cyclic symmetry procedure (MSOPT and CECYCMS commands). The inter-sector spring of stiffness c is split into two springs (COMBIN14) of stiffness 2*c in order to apply the cyclic CEs. Inside the sector, the linear oscillator is modeled by COMBIN14 and a unit mass MASS21. The nonlinear spring is created using a user-defined element (USER300).

The model is solved using the harmonic balance method with three harmonics (HROPT ,HBM,3) using a frequency range from 90 to 100 Hz. The root mean square amplitude of the displacement is obtained for each calculated frequency by combining the different harmonics displacements.

Only cyclic harmonic index 0 response is excited, so the displacement amplitudes of all the masses are the same.

Results Comparison

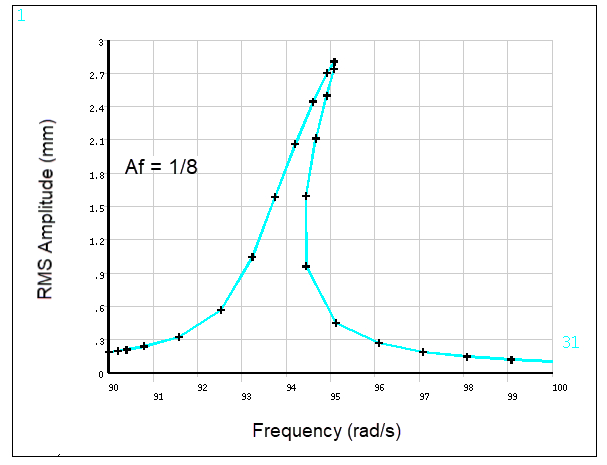
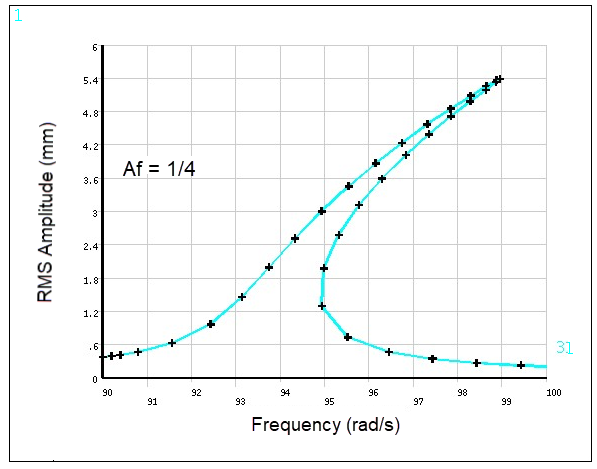
The maximum amplitude and the corresponding frequency for two different amplitudes of excitation Af are compared against numerical results from Grolet et al. (2011).

Figure 583: Nonlinear Harmonic Analysis of a Cyclic Chain of Oscillators (Af = 1/8)

Figure 584: Nonlinear Harmonic Analysis of a Cyclic Chain of Oscillators (Af = 1/4)