VM304

VM304
Sloshing Modes in a Hollow Cylindrical Cavity

Overview

Reference:	Robert D. Blevins. Formulas for Natural Frequency and Mode Shape. Krieger, 2001.
Analysis Type(s):	Modal Analysis (ANTYPE = 2)
Element Type(s):	3D 20-Node Acoustic Solid (FLUID220) 3D 20-Node Structural Solid (SOLID186)
Input Listing:	vm304.dat VM304 requires a supplemental .cdb input file which is too long to include full input listings. This file must be downloaded and placed in your working directory for the test case to run properly. Additionally, the geometry and mesh should be regenerated. Download link: MAPDL Test Case Files for 2024 R2 vm304.cdb

Test Case

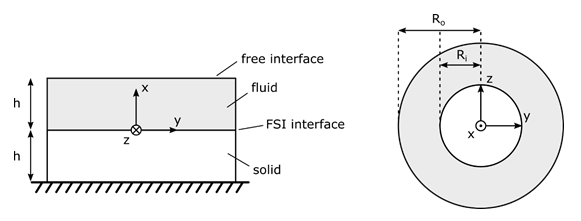
The cavity consists of two stacked hollow cylinders. The bottom cylinder is made of steel. The top cylinder contains water.

Both cylinders have inner radius Ri and outer radius Ro. The bottom of the lower cylinder is clamped.

Fluid-Structure Interaction (FSI) at the interface between fluid and solid is considered.

The fluid lateral boundary is a rigid wall and the top surface is free.

Figure 550: Problem Sketch

Figure 551: Finite Element Model

Material Properties	Geometric Properties
For fluid: Speed of sound c0 = 1500 m/s Density ρ_f = 1000 kg/m³ For solid: Young’s modulus E = 1.44 x 10¹¹ Pa Poisson’s ratio ν = 0.35 Density ρ_s = 7700 kg/m³	Inner radius Ri = 0.1 m Outer radius Ro = 0.2 m Height h = 0.1 m

Material Properties

Geometric Properties

For fluid:

Speed of sound c0 = 1500 m/s

Density ρ_f = 1000 kg/m³

For solid:

Young’s modulus E = 1.44 x 10¹¹ Pa

Poisson’s ratio ν = 0.35

Density ρ_s = 7700 kg/m³

Inner radius Ri = 0.1 m

Outer radius Ro = 0.2 m

Height h = 0.1 m

Analysis Assumptions and Modeling Notes

In Mechanical APDL, pressure in a fluid medium is determined by the acoustic wave equation; therefore, the pressure considered is the excess pressure from the mean pressure. That pressure is used in the modal analysis to determine the sloshing frequencies and mode shapes.

Results Comparison

First 10 Natural Frequencies
(i, j) [1]	Target	Mechanical APDL	Ratio
(0,1)	0.9963	0.9963	1.000
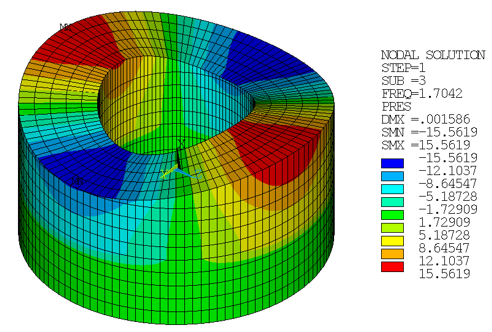
(0,2)	1.7042	1.7042	1.000
(0,3)	2.1755	2.1756	1.000
(0,4)	2.5214	2.5215	1.000
(0,5)	2.8064	2.8016	0.998
(1,0)	2.8184	2.8140	0.998
(1,1)	2.8560	2.8523	0.999
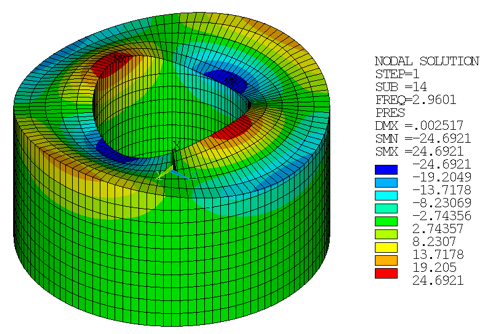
(1,2)	2.9623	2.9601	0.999
(0,6)	3.0449	3.0435	1.000
(1,3)	3.1210	3.1203	1.000

i = number of nodal circles, and j = number of nodal diameters.

Figure 552: Mode Shape (0,2)

Figure 553: Mode Shape (1,2)