VM293
VM293
Evaluation of Stress Intensity Factor KI Using the Unstructured
Mesh Method (UMM)
Overview
| Reference: | Rice, J.R., Mathematical Analysis in the Mechanics of Fracture, Chapter 3, pg. 222, 1968 |
| Analysis Type(s): | Static Analysis (ANTYPE = 0) |
| Element Type(s): | 3D 4-Node Tetrahedral Structural Solid with Nodal Pressures (SOLID285) |
| Input Listing: | vm293.dat |
|
VM293 includes a supplemental .cdb input file which is too long to include full input listings. This file must be downloaded and placed in your working directory for the test case to run properly. Additionally, the geometry and mesh should be regenerated. Download link: MAPDL Test Case Files for 2024 R2 vm293.cdb |
Test Case
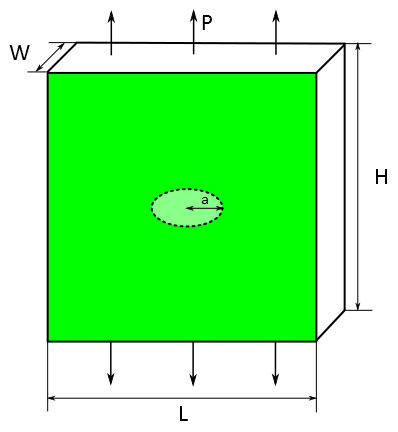
A rectangular block with an embedded penny-shaped crack is subjected to a tensile stress, P, as shown in the problem sketch. Symmetry boundary conditions are considered in this analysis. The stress intensity factor KI is determined using the CINT command.
| Material Properties | Geometric Properties | Loading | ||||||
|---|---|---|---|---|---|---|---|---|
|
| Uniform tension (applied to top and bottom surfaces), P = 100 MPa |
Analysis Assumptions and Modeling Notes
The problem is sovled using 3D 4-node tetrahedral structural elements (SOLID285). Because of symmetry conditions implied in the problem, on 1/8 of the model is analyzed. The block is subjected to a tensile stress and the stress intensity factor KI is computed at the crack tip nodes. The crack front and the path surrounding the crack front are defined using the CINT command. The computed stress intensity factor is then compared against the reference solution.
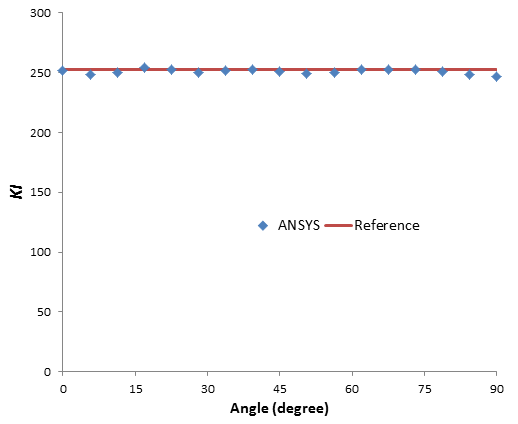
Results Comparison
| Crack Tip Node | Target | Mechanical APDL | Ratio |
|---|---|---|---|
| 236 | 252.30 | 252.36 | 1.000 |
| 242 | 252.30 | 247.22 | 0.980 |
| 243 | 252.30 | 247.85 | 0.982 |
| 244 | 252.30 | 249.75 | 0.990 |
| 245 | 252.30 | 254.79 | 1.010 |
| 246 | 252.30 | 252.71 | 1.002 |
| 247 | 252.30 | 250.44 | 0.993 |
| 248 | 252.30 | 252.45 | 1.001 |
| 249 | 252.30 | 253.46 | 1.005 |
| 250 | 252.30 | 251.81 | 0.998 |
| 251 | 252.30 | 249.72 | 0.990 |
| 252 | 252.30 | 250.74 | 0.994 |
| 253 | 252.30 | 252.72 | 1.002 |
| 254 | 252.30 | 253.36 | 1.004 |
| 255 | 252.30 | 253.26 | 1.004 |
| 256 | 252.30 | 250.97 | 0.995 |
| 257 | 252.30 | 248.05 | 0.983 |